1.4 Aplicaciones de la integral definida.
1.4.4 Volúmenes por secciones transversales.
Existen sólidos que no se obtienen del giro de una región con respecto a un eje, para determinar el volumen de estos sólidos se emplea el método de secciones transversales, llamado también rebanadas. La idea de este método es el de tomar el sólido con respecto a uno de sus ejes y cortarlo en “rebanadas”, para posteriormente calcular el volumen de cada rebanarla y sumarlas.
Supongamos que se quiere hallar el volumen de un sólido \(S\) como el que se muestra a continuación, primero trazaremos los ejes \(x\) y \(y\) para referencia, y a su vez cortaremos el sólido con un plano obteniendo así la sección transversal que es perpendicular al eje \(x\) y que pasa por el punto \(x\), donde \(a \leq x \leq b\) y el área de la sección transversal es \(A(x)\) y varia conforme lo hace \(x\).

Si se divide el sólido \(S\) en \(n\) rebanadas de ancho igual a \(\Delta x\), esto es una partición del intervalo \([a, b]\) a lo largo del eje \(x\).

Consideremos el intervalo \([x_{i-1}, x_{i}]\) y determinemos el volumen de la i-ésima rebanada \(V_{i}\). El volumen \(V_{i}\) de la rebanada es igual al área de la sección transversal \(A_{i}(x)\) por su altura \(\Delta x\), esto es: \[ V_{i}(x) = A_{i}(x) \Delta x \] Calculando los volúmenes para cada subintervalo y sumándolos, tenemos: \[ V \approx \sum_{i=1}^{n} A(x_{i}) \Delta x \] Tomando el límite cuando \(n\) tiende a infinito, se tiene que el volumen del sólido es: \[ V = \lim_{n\to\infty} \sum_{i=1}^{n} A(x_{i}) \Delta x = \int_{a}^{b} A(x) \,dx \]
El volumen del sólido \(S\) con área de la sección transversal igual a \(A(x)\), desde \(x=a\) hasta \(x=b\), perpendicular al eje \(x\) es: \[ V = \int_{a}^{b} A(x) \,dx \] El volumen del sólido \(S\) con área de la sección transversal igual a \(A(y)\), desde \(y=c\) hasta \(y=d\), perpendicular al eje \(y\) es: \[ V = \int_{c}^{d} A(y) \,dy \]
Ejemplo 1.
Determinar el volumen de la pirámide recta de altura \(h\) y base cuadrada de lado \(a\). Consideraremos la pirámide de manera horizontal y hacia la derecha, esto para poder ubicar el eje \(x\) como el eje de la pirámide, de tal manera que el eje \(x\) se posicione en el centro de ella sobre la base, tal y como se puede apreciar en la siguiente figura:

Asimismo, trazaremos la sección transversal perpendicular al eje \(x\), a una distancia \(x\) del origen, esta sección es un cuadrado de lado \(l\). Para determinar el volumen necesitamos determinar el área de la sección y posteriormente calcular el volumen con la integral de la sección de \(0\) hasta \(h\), ya que \(x\) se puede tomar desde el vértice de la pirámide hasta la base.
El área de la sección transversal es \(A(l) = l^2\), por lo que necesitamos expresar \(l\) en términos de la variable \(x\) y en dado caso de las constantes. Para ello podemos tomar el triángulo que se forma del origen a la base de la pirámide que pasa por la sección transversal, como se muestra en la siguiente figura:

Por triángulos semejantes tenemos: \[ \frac{x}{h} = \frac{\frac{1}{2}}{\frac{a}{2}} \:\:de\:\:donde\:\: \frac{x}{h} = \frac{l}{a} \:\:y\:\: l=\frac{ax}{h} \] Tomando en cuenta que: \[ A(x) = \left( \frac{ax}{h} \right)^2 = \frac{a^2}{h^2} x^2 \] Por lo tanto: \[ V = \int_{0}^{h} \frac{a^2}{h^2} x^2 \,dx = \frac{a^2}{h^2} \int_{0}^{h} x^2 \,dx = \frac{a^2}{h^2} \left( \frac{1}{3} x^3 \right) \Big|_{0}^{h} \] \[ \Rightarrow \frac{a^2}{h^2} \left( \frac{1}{3}h^3 - 0\right) = \frac{1}{3}a^2 h\]
Concluimos entonces que el volumen de la pirámide recta de altura \(h\) y base cuadrada de lado \(a\) es. \[ V = \frac{1}{3}a^2 h \]
Ejemplo 2.
Un tetraedro tiene tres caras perpendiculares entre sí y tres aristas también perpendiculares de \(2\:cm\), \(3\:cm\) y \(4\:cm\) de longitud respectivamente. Calcular el volumen. Para resolver el problema necesitamos trazar una sección transversal del sólido, para ello necesitamos esbozar el sólido.
Un tetraedro es un poliedro de cuatro caras donde cada cara es un triángulo, para tener una idea más precisa, un tetraedro que conocemos es el boing de triangulito. Eso ya nos da una idea del sólido, la otra indicación que nos dan es que tiene tres caras perpendiculares y tres aristas perpendiculares esto es, tres lados perpendiculares, posteriormente ubicaremos el tetraedro en el plano \(x,y,z\), tomando a este como base del sólido y las rectas que van del eje \(x\) al eje \(y\), del eje \(y\) al eje \(z\) y del eje \(z\) al eje \(x\), así:

Consideremos a \(z\) como el eje del tetraedro así las secciones transversales serán perpendiculares a \(z\) y la variable para integrar también es \(z\). Trazando la sección a una distancia \(z\), tenemos la siguiente figura:
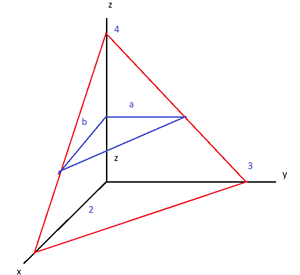
La sección transversal es un triángulo rectángulo digamos de catetos \(a\) y \(b\), por lo que el área de la sección sería \(A = \frac{1}{2} ab\), necesitamos expresar \(a\) y \(b\) en términos de la variable \(z\). Para ello usaremos triángulos semejantes.
Por triángulos semejantes tenemos: \[ \frac{b}{2} = \frac{4-z}{4} \] De donde: \[ b = \frac{4-z}{2} \]
Tomamos el triángulo sobre el eje \(x\) y el eje \(z\):

Por triángulos semejantes tenemos \[ \frac{a}{3} = \frac{4-z}{4} \] De donde: \[ a = 3 \left( \frac{4-z}{4} \right) = \frac{3}{4}(4-z) \] Luego: \[ A(z) = \frac{1}{2} \left( \frac{3}{4} (4-z) \right) \left( \frac{4-z}{2} \right) = \frac{3}{16}(4-z)^2 \]
Tomando ahora el triángulo sobre el eje \(y\) y el eje \(z\):

Por lo tanto: \[ V = \int_{0}^{4} \frac{3}{16} (4-z)^2 \,dz = \frac{3}{16} \int_{0}^{4} (4-z)^2 \,dz \] \[ \Rightarrow - \frac{3}{16} \left( \frac{1}{3} \right) (4-z)^3 \Big|_{0}^{4} = - \frac{1}{16} \left[ (4-4)^3 - (4-0)^3 \right] \] \[ \Rightarrow -\frac{1}{16} (-64) = 4\] Entonces el volumen del tetraedro que tiene tres caras perpendiculares entre sí y tres aristas también perpendiculares de \(2\:cm\), \(3\:cm\) y \(4\:cm\) de longitud respectivamente es: \[ \therefore V = 4 \]
Ejemplo 3.
Otro tipo de ejercicios que podemos encontrar es cuando no podemos dar la descripción del sólido mediante un objeto conocido, para ese caso se da una descripción del sólido mediante su base y las secciones transversales. Un ejemplo de este tipo es el siguiente.
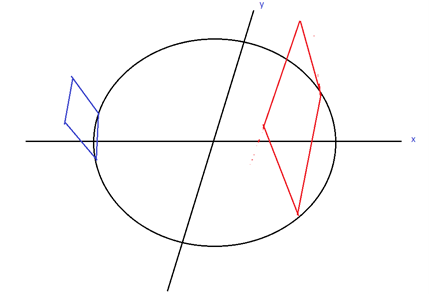
La base de un sólido es la región circular contenida en el plano \(xy\) acotada por la gráfica de \(x^{2}+y^{2}=a^{2}\) done \( a \gt 0 \). Calcular el volumen del sólido suponiendo que todas las secciones transversales correspondientes a planos perpendiculares al eje \(x\) son cuadrados.
En la siguiente figura se representa la base circular del sólido y dos secciones transversales perpendiculares al eje \(x\).
Como la sección transversal es un cuadrado, el área es \(A(l) = l^{2}\), hay que determinar \(l\) en términos de la variable \(x\), ya que la sección es perpendicular al eje \(x\). Para ello consideremos el círculo y el lado de una sección sobre él, como se observa en la siguiente figura:
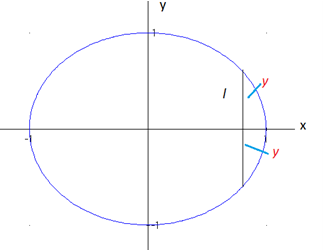
Por la simetría de la circunferencia se tiene que el lado del cuadrado es igual a \(2y\), así: \[ A = (2y^{2}) = 4y^{2} \] Necesitamos que el área sea función de \(x\) y tenemos que la ecuación de la circunferencia es \(x^{2}+y^{2}=a^{2}\), de donde: \[ y^{2} = a^{2} - x^{2} \] \[ A(x) = 4(a^{2} - x^{2}) \]
La sección transversal se toma desde \(x=-a\) hasta \(x=a\), así entonces: \[ V = \int_{-a}^{a} 4(a^{2} - x^{2})\,dx = 2 \int_{0}^{a} 4(a^{2} - x^{2})\,dx \] \[ V = 8 \left( a^{2}x - \frac{1}{3}x^{3} \right)\Bigg|_{0}^{a} = 8 \left( a^{3} - \frac{1}{3}a^{3} \right) = \frac{16}{3}a^{3} \] \[ \therefore V = \frac{16}{3}a^{3} \]