2.1 Formas indeterminadas

2.1.2 Cocientes indeterminados \( (\frac{0}{0}, \frac{\infty}{\infty} )\) y la Regla de L'Hôpital

En el estudio del cálculo con frecuencia aparecen límites de la forma donde ambas funciones \(f(x)\) y \(g(x)\) tienen límite \(0\) cuando \(x\) tiende a \(c\). En consecuencia, se dice que \(\frac{f(x)}{g(x)}\) tienen la forma indeterminada \(\frac{0}{0}\) en \(x=c\). Por otro lado, si los límites de \(f(x)\) y \(g(x)\) son \(\infty\) o bien \(-\infty\) cuando \(x\) tiende a \(c\), se dice \(\frac{f(x)}{g(x)}\) tiene la forma indeterminada \(\frac{\infty}{\infty}\) en \(x=c\).

Los cocientes indeterminados se tienen presentes en límites como los siguientes: \[ \lim_{x \to 2} \frac{x^2-4}{3x-6}, \lim_{x \to \infty} \frac{x^4-3x^3+5x^2-3x+8}{(x^2-2)^2}, \lim_{x \to 0} \frac{3^x-1}{x}, \lim_{x \to 0} \frac{\tan x - x}{x^3}, \lim_{x \to \infty} \frac{e^{x^2}}{x^2} \] De los cuales se obtienen las siguientes formas indeterminadas \[ \frac{0}{0}, \frac{\infty}{\infty}, \frac{0}{0}, \frac{0}{0}, \frac{\infty}{\infty}, \:\: respectivamente. \] En el caso de los dos primeros límites \( \lim\limits_{x \to 2} \frac{x^2-4}{3x-6}, \lim\limits_{x \to \infty} \frac{x^4-3x^3+5x^2-3x+8}{(x^2-2)^2} \) es posible calcularlos usando técnicas algebraicas, pero los límites \( \lim\limits_{x \to 0} \frac{3^x-1}{x}, \lim\limits_{x \to 0} \frac{\tan x - x}{x^3}, \lim\limits_{x \to \infty} \frac{e^{x^2}}{x^2} \) no se pueden determinar usando procedimientos algebraicos, esto es debido a que en ellos combinamos las funciones algebraicas con las funciones transcendentes, por lo que necesitaremos otra técnica para su solución. Esta otra técnica se denomina Regla de L'Hôpital, pero para poder llegar a su definición y comprender cómo surgió, es importante que revisemos primero la Fórmula de Cauchy.

Demostración. La primer condición que se debe cumplir es que \(g(b)-g(a) \neq 0\), ya que de acuerdo al Teorema de Rolle si una función \(f\) es continua en el intervalo cerrado \([a, b]\), derivable en el intervalo abierto \((a, b)\) y \(f(a)=f(b)\), entonces existe al menos un número \(c\) en \((a, b)\) tal que \(f'(c)=0\). Por lo que si existe un número \(c\) en \((a, b)\) tal que \(g'(c)=0\), entonces se contradice la hipótesis sobre \(g'(x)\).

Sea \(h\) una nueva función definida de la siguiente manera: \[ h(x)=[f(b)-f(a)]g(x)-[g(b)-g(a)]f(x) \:\: \forall x \:\:en\:\: [a, b] \] \begin{array}{rcl} h(a)&=&[f(b)g(a)-f(a)g(a)]-[g(b)f(a)-g(a)f(a)]\\ h(a)&=&[f(b)g(a)-g(b)f(a)] \end{array} \begin{array}{rcl} h(b)&=&[f(b)g(b)-f(a)g(b)]-[g(b)f(b)-g(a)f(b)] \\ h(b)&=&[g(a)f(b)-f(a)g(b)] \end{array} Por lo tanto, se tiene que \(h(a)=h(b)\).

Dado que \(f\) y \(g\) son continuas en \([a, b]\) y derivables en \((a, b)\), se deduce que \(h\) es continua en \([a, b]\), derivable en \((a, b)\) y por el Teorema de Rolle existe un número \(w\) en \((a, b)\) tal que \(h'(w) = 0\), es decir: \[ h'(w)=[f(b)-f(a)]g'(w)-[g(b)-g(a)]f'(w)=0 \] En consecuencia tenemos que: \[ \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(w)}{g'(w)} \] Para el caso particular en el que \(g(x)=x\) se tiene que: \[ \frac{f(b)-f(a)}{b-a} = \frac{f'(w)}{1} \] Realizando un despeje nos damos cuenta que obtenemos el Teorema del Valor Medio: \[ f(b)-f(a) = f'(w)(b-a) \] Lo anterior demuestra que la fórmula de Cauchy es una generalización del Teorema del Valor Medio

Como ya vimos anteriormente es posible eliminar la indeterminación de un límite utilizando alguna técnica algebraica, pero ahora introduciremos la Regla de L'Hôpital.

Demostración. Supongamos que \(\lim\limits_{x \to c} \frac{f(x)}{g(x)} = \frac{0}{0} \) y que \(\lim\limits_{x \to c} \frac{f'(x)}{g'(x)} = L \) para un número real \(L\). Se quiere demostrar que: \begin{equation} \lim_{x \to c} \frac{f(x)}{g(x)} = L \end{equation}

Sean \(F\) y \(G\) tales que: \[ F(x) = f(x) \:\: si \:\: x \neq c \:\:y\:\: F(c)=0 \] \[ G(x) = g(x) \:\: si \:\: x \neq c \:\:y\:\: G(c)=0 \] Como \(\lim\limits_{x \to c} F(x) = \lim\limits_{x \to c} f(x) = 0 = F(c)\) la función \(F\) es continua en \(c\) y por lo tanto es continua en todo el intervalo \((a, b)\); además \(F'(x) = f'(x)\) y \(G'(x) = g'(x)\) siempre que \(x \neq c\).

Aplicando la fórmula de Cauchy a los intervalos \([c,x]\) o \([x,c]\) resulta que existe un número \(w\) entre \(c\) y \(x\) tal que: \[ \frac{F(x)-F(c)}{G(x)-G(c)} = \frac{F'(w)}{G'(w)} = \frac{f'(w)}{g'(w)} \] Aprovechando el hecho de que \(F(x)=f(x), G(x)=g(x) \:\:y\:\: F(c)=G(c)=0\), se tiene que: \[ \frac{f(x)}{g(x)} = \frac{f'(w)}{g'(w)} \] Y como \(w\) se encuentra entre \(c\) y \(x\) resulta que: \[ \lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(w)}{g'(w)} = L \]

Ejemplo 1. Determinar el valor del límite si es que existe.

\[ \lim_{x \to 2} \frac{x^2-4}{3x-6} \] Al evaluar el límite vemos que obtenems una forma indeterminada. \[ \lim_{x \to 2} \frac{x^2-4}{3x-6} = \frac{0}{0} \] Veamos si podemos calcular el valor del límite usando técnicas algebraicas: \[ \lim_{x \to 2} \frac{x^2-4}{3x-6} = \lim_{x \to 2} \frac{(x-2)(x+2)}{3(x-2)} = \lim_{x \to 2} \frac{x+2}{3} = \frac{4}{3} \] Asimismo, verifiquemos el resultado utilizando la regla de L'Hôpital: \[ \lim_{x \to 2} \frac{x^2-4}{3x-6} = \lim_{x \to 2} \frac{2x}{3} = \frac{4}{3} \] Como podemos observar, utilizando técnicas algebraicas o la regla de L'Hôpital obtenemos el mismo resultado.

Ejemplo 2. Determinar el valor del límite si es que existe.

\[ \lim_{x \to \infty} \frac{x^4-3x^3+5x^2-3x+8}{(x^2-2)^2} \] Al evaluar el límite se tiene una forma indeterminada: \[ \lim_{x \to \infty} \frac{x^4-3x^3+5x^2-3x+8}{(x^2-2)^2} = \frac{\infty}{\infty} \] Resolviendo algebraicamente tenemos lo siguiente: \[ \lim_{x \to \infty} \frac{x^4-3x^3+5x^2-3x+8}{(x^2-2)^2} = \lim_{x \to \infty} \frac{\frac{x^4-3x^3+5x^2-3x+8}{x^4}}{\frac{(x^2-2)^2}{x^4}} \] \[ \Rightarrow \lim_{x \to \infty} \frac{1-\frac{3}{x}+\frac{5}{x^2}-\frac{3}{x^3}+\frac{8}{x^4}}{\left( 1 - \frac{2}{x^2} \right)^2} = \lim_{x \to \infty} \frac{1-\frac{3}{x}+\frac{5}{x^2}-\frac{3}{x^3}+\frac{8}{x^4}}{\left( 1 - \frac{2}{x^2} \right)^2} \] \[ \Rightarrow \frac{1-\frac{3}{\infty}+\frac{5}{\infty^2}-\frac{3}{\infty^3}+\frac{8}{\infty^4}}{\left( 1 - \frac{2}{\infty^2} \right)^2} = 1 \] Utilizando la regla de L'Hôpital tenemos: \[ \lim_{x \to \infty} \frac{x^4-3x^3+5x^2-3x+8}{(x^2-2)^2} \] \[ \Rightarrow \lim_{x \to \infty} \frac{4x^3-9x^2+10x-3}{2(x^2-2)2x} \] \[ \Rightarrow \lim_{x \to \infty} \frac{4x^3-9x^2+10x-3}{4x(x^2-2)} \] Al evaluar el límite después de aplicar la regla de L'Hôpital vemos que aún obtenemos una indeterminación: \[ \lim_{x \to \infty} \frac{4x^3-9x^2+10x-3}{4x(x^2-2)} = \frac{\infty}{\infty} \] Apliquemos nuevamente la regla de L'Hôpital: \[ \lim_{x \to \infty} \frac{4x^3-9x^2+10x-3}{4x^3-8x} = \lim_{x \to \infty} \frac{12x^2-18x+10}{12x^2-8} = \frac{\infty}{\infty} \] Tal y como podemos observar aún seguimos teniendo una indeterminación, por lo que volveremos a aplicar la regla de L'Hôpital: \[ \lim_{x \to \infty} \frac{12x^2-18x+10}{12x^2-8} = \lim_{x \to \infty} \frac{24x-18}{24x} = \frac{\infty}{\infty} \] El resultado obtenido aún es una indeterminación, por lo que podemos tratar de aplicar la regla de L'Hôpital una vez más: \[ \lim_{x \to \infty} \frac{24x-18}{24x} = \lim_{x \to \infty} \frac{24}{24} = 1 \] Por lo tanto: \[ \lim_{x \to \infty} \frac{x^4-3x^3+5x^2-3x+8}{(x^2-2)^2} = 1 \] Como pudimos observar, no siempre usar la regla de L’Hôpital nos da el procedimiento más directo para determinar el valor del límite de una función. Pero cuando se trata de una función trascendente o una compuesta por funciones transcendentes y algebraicas, no es posible resolverlo con técnicas algebraicas, por lo que es imprescindible usar la regla de L'Hôpital.

Ejemplo 3. Calcular el límite de la siguiente función.

\[ y = \lim_{x \to 0} \frac{e^x-1}{x} \] Al evaluar el límite se tiene una forma indeterminada: \[ \lim_{x \to 0} \frac{e^x-1}{x} = \frac{e^0-1}{0} = \frac{0}{0} \] Por lo que procederemos a aplicar la regla de L'Hôpital (derivando el numerador y el denominador): \[ \lim_{x \to 0} \frac{e^x-1}{x} = \lim_{x \to 0} \frac{e^x}{1} = \frac{e^0}{1} = \frac{1}{1} = 1 \] Como se puede observar en la gráfica cuando \(x\) se acerca a cero, por la derecha o por la izquierda, la función se aproxima \(1\).

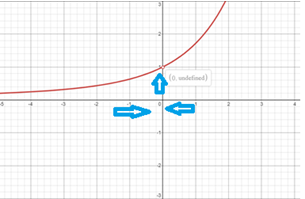
Ejemplo 4. Calcular el límite de la siguiente función.

\[ y = \lim_{x \to 1} \frac{x^3-3x+2}{1-x+\ln(x)} \] Al evaluar el límite se tiene una indeterminación de cociente, por lo que procederemos a aplicar la regla de L'Hôpital. La regla de L’Hôpital se puede aplicar sucesivamente siempre y cuando se trate de cocientes indeterminados \[ \lim_{x \to 1} \frac{x^3-3x+2}{1-x+\ln(x)} = \lim_{x \to 1} \frac{3x^2-3}{-1+\frac{1}{x}} \] Aplicando el valor al cual tiende \(x\) en el límite, vemos que obtenemos nuevamente una indeterminación de cocientes: \[ \lim_{x \to 1} \frac{3x^2-3}{-1+\frac{1}{x}} = \frac{3-3}{0} = \frac{0}{0} \] Como se obtuvo una indeterminación de cociente, podemos volver a aplicar la Regla de L'Hôpital \[ \lim_{x \to 1} \frac{3x^2-3}{-1+\frac{1}{x}} = \lim_{x \to 1} \frac{6x}{-\frac{1}{x^2}} \] Se sustituye por \(1\) que es el valor al que tiende \(x\) para así obtener el valor del límite: \[ \lim_{x \to 1} \frac{6x}{-\frac{1}{x^2}} = \frac{6}{-1} = -6 \] En la siguiente gráfica se observa que cuando \(x\) se aproxima a \(1\) la función se aproxima a \(-6\).

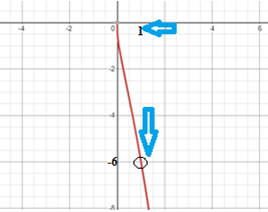
Ejercicios complementarios de la sección.

1. Determina el límite si es que existe de: \[ \lim_{x \to 1} \frac{x^{a}-ax+a-1}{(x-1)^{2}} \] Evaluando en \(1\) tenemos que: \[ \frac{1^{a}-a(1)+a-1}{(1-1)^{2}} = \frac{1-a+a-1}{(0)^{2}} = \frac{0}{0} \] Vemos que obtenemos una indeterminación de cociente, por lo que podemos aplicar la regla de L'Hôpital: \[ \lim_{x \to 1} \frac{ \displaystyle\frac{dy}{dx} \Big(x^{a}-ax+a-1\Big)}{ \displaystyle\frac{dy}{dx} (x-1)^{2}} = \lim_{x \to 1} \frac{ax^{a-1}-a}{2x-2} \] Evaluando en \(1\) tenemos que: \[ \frac{a(1)^{a-1}-a}{2(1)-2} = \frac{a-a}{2-2} = \frac{0}{0} \] Vemos que obtenemos una indeterminación de cociente, por lo que podemos aplicar la regla de L'Hôpital nuevamente: \[ \lim_{x \to 1} \frac{ \displaystyle\frac{dy}{dx} \Big(ax^{a-1}-a\Big)}{ \displaystyle\frac{dy}{dx} \Big(2x-2\Big)} = \lim_{x \to 1} \frac{(a^{2}-1)x^{a-2}}{2} \] Evaluando el límite tenemos que: \[ \frac{(a^{2}-1)(1)^{a-2}}{2} = \frac{a^{2}-1}{2} \] Por lo tanto el límite queda como sigue: \[ \lim_{x \to 1} \frac{x^{a}-ax+a-1}{(x-1)^{2}} = \frac{a^{2}-1}{2} \]

2. Determina el límite si es que existe de: \[ \lim_{x \to 0} \frac{\cos{(x)} -1 + \displaystyle\frac{1}{2}x^{2}}{x^{4}} \] Evaluando el límite en cero tenemos que: \[ \frac{\cos{(0)} -1 + \displaystyle\frac{1}{2}(0)^{2}}{(0)^{4}} = \frac{1-1+0}{0} = \frac{0}{0} \] Vemos que obtenemos una indeterminación de cociente, por lo que podemos aplicar la regla de L'Hôpital: \[ \lim_{x \to 0} \frac{ \displaystyle\frac{dy}{dx} \left(\cos{(x)} -1 + \displaystyle\frac{1}{2}x^{2}\right)}{\displaystyle\frac{dy}{dx} \Big(x^{4}\Big)} = \lim_{x \to 0} \frac{-\sin{(x)} + \displaystyle\frac{1}{2}(2x)}{4x^{3}} \] Evaluamos nuevamente el límite: \[ \frac{-\sin{(0)} + 0}{4(0)^{3}} = \frac{0}{0} \] Vemos que podemos aplicar L'Hôpital hasta desaparecer la variable del denominador que causa la indeterminación: \[ \lim_{x \to 0} \frac{ \displaystyle\frac{dy}{dx} \Big(-\sin{(x)} + x\Big)}{\displaystyle\frac{dy}{dx} \Big(4x^{3}\Big)} = \lim_{x \to 0} \frac{ \displaystyle\frac{dy}{dx} \Big(-\cos{(x)} + 1\Big)}{\displaystyle\frac{dy}{dx} \Big(12x^{2}\Big)} \] \[ = \lim_{x \to 0} \frac{ \displaystyle\frac{dy}{dx} \Big(\sin{(x)} \Big)}{\displaystyle\frac{dy}{dx} \Big(24x\Big)} = \lim_{x \to 0} \frac{\cos{x}}{24} \] Finalmente, evaluando el límite tenemos que: \[ \frac{\cos{0}}{24} = \frac{1}{24} \] Por lo tanto el límite queda como sigue: \[ \lim_{x \to 0} \frac{\cos{(x)} -1 + \displaystyle\frac{1}{2}x^{2}}{x^{4}} = \frac{1}{24} \]

3. Hallar los valores de \(a\) y \(b\) tales que: \[ \lim_{x \to 0} \frac{\sin{(2x)}+ax+bx^{3}}{x^{3}} = 0 \] Evaluando el límite obtenemos lo siguiente: \[ \frac{\sin{(2(0))}+a(0)+b(0)^{3}}{(0)^{3}} = \frac{\sin{(0)}+0+0}{0} = \frac{0}{0} \] Al obtener una forma indeterminada de cociente podemos aplicar la regla de L'Hôpital: \[ \lim_{x \to 0} \frac{\displaystyle\frac{dy}{dx} \Big(\sin{(2x)}+ax+bx^{3}\Big)}{ \displaystyle\frac{dy}{dx} \Big(x^{3}\Big)} = \lim_{x \to 0} \frac{2\cos{(2x)}+a+3bx^{2}}{3x^{2}} \] Evaluamos el límite: \[ \frac{2\cos{2(0)}+a+3b(0)^{2}}{3(0)^{2}} = \frac{2+a}{0} \] Si \(2+a\) es un número real \(n\) diferente de cero el límite no existiría ya que se tendría \( \displaystyle\frac{n}{0} = \pm\infty \), pero el problema indica que el límite si existe porque vale \(0\), de modo que la única opción para el numerador es que sea cero, esto es: \[ 2 + a = 0 \;luego\; a = -2\] Realizando el cambio vemos que nuevamente obtenemos una forma indeterminada, por lo que volvemos a aplicar la regla de L'Hôpital y se tiene: \[ \lim_{x \to 0} \frac{\displaystyle\frac{dy}{dx} \Big(2\cos{(2x)}+a+3bx^{2}\Big)}{\displaystyle\frac{dy}{dx}\Big(3x^{2}\Big)} = \lim_{x \to 0} \frac{-4\sin{(2x)} + 6bx}{6x} \] Evaluamos el límite: \[ \frac{-4\sin{2(0)} + 6b(0)}{6(0)} = \frac{0}{0} \] Podemos volver a aplicar la regla de L'Hôpital: \[ \lim_{x \to 0} \frac{ \displaystyle\frac{dy}{dx}\Big( -4\sin{(2x)} + 6bx \Bigg)}{\displaystyle\frac{dy}{dx}\Big(6x\Big)} = \lim_{x \to 0} \frac{-8\cos{(2x)} + 6b}{6} \] Finalmente, evaluamos el límite: \[ \frac{-8\cos{(2(0))} + 6b}{6} = \frac{-8+6b}{6} \] Así, tenemos que el valor del límite es \( \displaystyle\frac{-8+6b}{6} \) y que es \(0\), luego: \begin{array} {rcl} \displaystyle\frac{-8+6b}{6} &=& 0 \\ -8+6b &=& 0 \\ 6b &=& 8 \\ b &=& \displaystyle\frac{8}{6} \\ b &=& \displaystyle\frac{4}{3} \end{array} Por lo tanto, los valores de \(a\) y \(b\) para los cuales el límite existe y vale \(0\) son: \[ a = -2 \;\;y\;\; b = \frac{4}{3} \]