2.1 Formas indeterminadas

2.1.3 Producto indeterminado

Definición. Un producto indeterminado se obtiene cuando al evaluar el límite de la función, obtenemos las formas \(0 \times \infty\) o \(0 \times -\infty\) y la estrategia de solución es modificar algebraicamente la función para convertirla a un cociente, lo que nos permite usar la Regla de L'Hôpital.

Ejemplo 1. Determinar el valor del límite si es que existe.

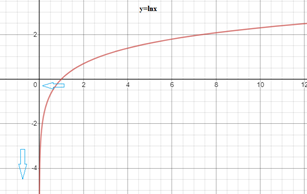
\[ y = \lim_{x \to 0^{+}} x \ln x \] Al evaluar el límite se obtiene una forma indeterminada de producto: \[ \lim_{x \to 0^{+}} x \ln x = 0^{+} \ln 0^{+} \] El valor de \(0^{+}\) es \(-\infty\) tal y como podemos observar en la gráfica, ya que cuando \(x\) se aproxima a cero por la derecha, los valores de la función \(\ln x\) crecen hacia los negativos, así \(\lim\limits_{x \to 0^+} \ln x = -\infty\).

De esta forma \(\lim\limits_{x \to 0^{+}} x \ln x = 0 \times -\infty\), que es una indeterminación de producto. Para remover la indeterminación, se requiere expresar a la función como un cociente, para que así podamos aplicar la regla de L'Hôpital ya que esta solo se ocupa sólo se ocupa para cocientes indeterminados no para otro tipo de indeterminaciones.

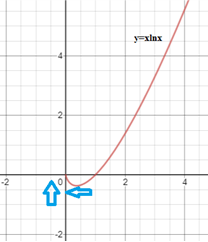
Entonces al transformar la función \(y = x \ln x\) en cociente (usando leyes de exponentes) y enseguida evaluando en cero, observamos que se obtiene una indeterminación de cociente: \[ \lim_{x \to 0^{+}} x \ln x = \lim_{x \to 0^{+}} \frac{\ln x}{x^-1} = \lim_{x \to 0^{+}} \frac{\ln x}{\frac{1}{x}} = \frac{-\infty}{\infty} \] Por lo que procedemos a aplicar la regla de L'Hôpital y se simplifica: \[ \lim_{x \to 0^{+}} \frac{\ln x}{\frac{1}{x}} = \lim_{x \to 0^{+}} \frac{\frac{1}{x}}{-\frac{1}{x^2}} = \lim_{x \to 0^{+}} - \frac{x^2}{x} \] Evaluamos el límite: \[ \lim_{x \to 0^{+}} - x = 0 \] Por lo tanto: \[ \lim_{x \to 0^{+}} x \ln x = 0 \] Como podemos observar en la siguiente gráfica cuando \(x\) se aproxima a \(0\) la función \(y = x \ln x\) se aproxima también a cero.

Con estos ejemplos notamos que:

1. Cuando obtenemos la forma de producto indeterminado para cambiar a un cociente realizamos el procedimiento: \[ \lim_{x \to a} f(x)g(x) = \lim_{x \to a} \frac{f(x)}{\frac{1}{g(x)}} \:\:o\:\:bien...\] \[ \lim_{x \to a} f(x)g(x) = \lim_{x \to a} \frac{g(x)}{\frac{1}{f(x)}} \] 2. Una vez que se aplicó la Regla de L'Hôpital se simplifica y después se evalúa.

Ejercicios complementarios de la sección.

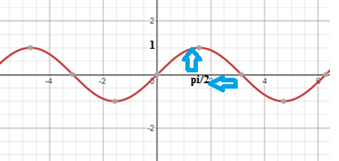
1. Determinar el límite de la función si es que existe. \[ \lim_{x \to \frac{\pi}{2}^{+}} \cos{x} \tan{x} = 0 \times \infty \] Al obtener una indeterminación de producto podemos expresar la función \(\tan{x}\) como cociente empleando la identidad trigonométrica \( \tan{x} = \displaystyle\frac{\sin{x}}{\cos{x}} \), después se cancelan términos semejantes. \[ \lim_{x \to \frac{\pi}{2}^{+}} \cos{x} \tan{x} = \lim_{x \to \frac{\pi}{2}^{+}} \cos{x} \displaystyle\frac{\sin{x}}{\cos{x}} = \lim_{x \to \frac{\pi}{2}^{+}} \sin{x} \] Se evalúa el límite en \( \displaystyle\frac{\pi}{2} \): \[ \sin{(\frac{\pi}{2})} = 1 \] En la siguiente gráfica se observa que para \( \displaystyle\frac{\pi}{2} \) la función tiene el valor de \(1\).

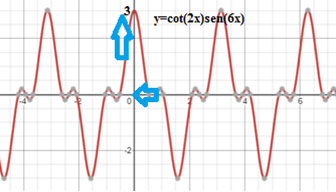
Por lo tanto, el valor del límite es: \[ \lim_{x \to \frac{\pi}{2}^{+}} \cos{x} \tan{x} = 1 \] 2. Determinar el límite de la función si es que existe. \[ \lim_{x \to 0} \cot{(2x)} \sin{(6x)} = 0 \times \infty \] Al obtener una indeterminación de producto podemos hacer uso de identidades trigonométricas para expresar como cociente la función, pero vemos que al evaluar se obtiene un cociente indeterminado: \[ \lim_{x \to 0} \frac{\sin{(6x)}}{\tan{(2x)}} = \frac{0}{0} \] Se aplica L'Hôpital y se evalúa. \[ \lim_{x \to 0} \frac{6 \cos{(6x)}}{2 \sec^{2}{(2x)}} = \frac{6}{2} = 3 \] Por lo tanto: \[ \lim_{x \to 0} \cot{(2x)} \sin{(6x)} = 3 \] En la siguiente gráfica se observa que al evaluar en \(0\) la función tiene el valor de \(3\).