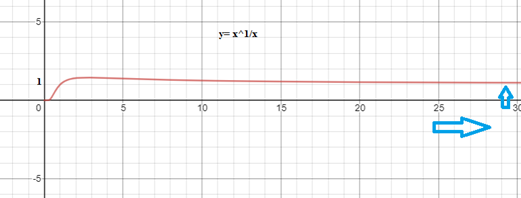2.1 Formas indeterminadas

2.1.5 Potencias indeterminadas

Definición. Las indeterminaciones de potencias surgen del \(\lim\limits_{x \to a} f(x)^{g(x)} \).

Para determinar el límite de una forma indeterminada de potencia procedemos de la siguiente forma:

1. Se toma la función \(y=(f(x))^{g(x)} \)

2. Se aplica logaritmo natural a ambos lados de la expresión, \(\ln (y) = \ln (f(x))^{g(x)} \)

3. Aplicando propiedades de los logaritmos se tiene que \(\ln (y) = g(x) \ln (f(x))\)

4. Se aplica el límite cuando \(x\) tiende a \(c\) a ambos lados de la ecuación, \(\lim\limits_{x \to c} [\ln⁡(y)] = \lim\limits_{x \to c} [g(x) \ln⁡(f(x)) ] \)

5. Al calcular el \(\lim\limits_{x \to c} [g(x) \ln⁡(f(x))] \) se tiene que:

a) Si \( \lim\limits_{x \to c} f(x) = 0 \) y \( \lim\limits_{x \to c} g(x) = 0 \) entonces: \[ \lim_{x \to c} [ g(x) \ln⁡(f(x)) ] = 0 \ln⁡(0) = 0(-\infty) \] b) Si \( \lim\limits_{x \to c} f(x) = \infty \) y \( \lim\limits_{x \to c} g(x) = 0 \) entonces: \[ \lim_{x \to c} [ g(x) \ln⁡(f(x)) ] = 0 \ln⁡(\infty) = 0(\infty) \] c) Si \( \lim\limits_{x \to c} f(x) = 1 \) y \( \lim\limits_{x \to c} g(x) = \infty \) entonces: \[ \lim_{x \to c} [ g(x) \ln⁡(f(x)) ] = \infty \ln⁡(1) = \infty(0) \] Como podemos ver cada caso nos lleva a una forma indeterminada de producto.

6. Si llamamos \(L\) al \(\lim\limits_{x \to c} [g(x) \ln⁡(f(x))] \) se tiene que \(\lim\limits_{x \to c} [\ln⁡(y)] = L\).

7. Aplicando la exponencial a ambos lados de la ecuación se tiene que: \[ e^{(\lim\limits_{x \to c} [\ln⁡(y)])} = e^{L} \] Es decir: \[ \lim_{x \to c} y = e^{L} \]

Ejemplo 1. Determinar el valor del límite si es que existe.

\[ y = \lim_{x \to 0} (1+\sin(4x))^{ctg (x)} \] Al evaluar el límite, obtenemos una indeterminación de potencia. \[ y = \lim_{x \to 0} (1+\sin(4x))^{ctg (x)} = 1^{\infty} \] Lo expresamos como una función y se obtiene el límite en ambos lados para no alterar la igualdad. \[ \lim_{x \to 0} y = \lim_{x \to 0} (1+\sin(4x))^{ctg (x)} \] Se obtiene \(\ln\) de las funciones en ambos lados de la ecuación: \[ \lim_{x \to 0} \ln y = \lim_{x \to 0} \ln (1+\sin(4x))^{ctg (x)} \] Por leyes de los logaritmos se expresa como un producto y se calcula el límite obteniéndose una indeterminación de producto: \[ \lim_{x \to 0} \ln y = \lim_{x \to 0} ctg (x) \ln (1+\sin(4x)) = (\infty)(0) \] Ahora la función se expresa como un cociente y se obtiene el límite, el cual termina siendo una indeterminación de cociente: \[ \lim_{x \to 0} \frac{\ln (1+\sin(4x))}{ctg (x)} = \frac{0}{0} \] Al tener una indeterminación de conociente podemos aplicar la regla de L'Hôpital: \[ \ln y = \lim_{x \to 0} \frac{4 \cos(4x)}{\frac{1+\,\sin(4x)}{sec^2(x)}} \Rightarrow \ln y = \lim_{x \to 0} \frac{4 \cos(4x)}{\sec^{2}(x) (1+\,\sin(4x))} = 4 \] Por definición de logaritmo sabemos que el logaritmo de un número es el exponente al que hay que elevar la base para obtener dicho número. En este caso el logaritmo natural de \(y\) es igual a \(4\), por lo que el \(4\) es el exponente de la base del logaritmo natural que es \(e\), por lo tanto: \[ \ln y = 4 \:\: entonces \:\: y = e^{4} \]

Ejemplo 2. Determinar el valor del límite si es que existe.

\[ y = \lim_{x \to 0} ( 1 + ax)^{\frac{b}{x}} \] Podemos observar que si \(f(x) = (1+ax)\) se tiene que \(\lim\limits_{x \to 0} f(x) = \lim\limits_{x \to 0} (1+ax) = 1\)

Y si \(g(x) = \frac{b}{x}\) se tiene que \(\lim\limits_{x \to 0} g(x) = \lim\limits_{x \to 0} \frac{b}{x} = \frac{b}{0} = \infty\), en consecuencia obtenemos una forma indeterminada de potencia. \[ y = \lim_{x \to 0} ( 1 + ax)^{\frac{b}{x}} = 1^{\infty} \] Para calcular el límite, primero construimos la función \(y = ( 1 + ax)^{\frac{b}{x}}\), aplicando logaritmo natural y propiedades del logaritmo, se obtiene \(\ln y = \frac{b}{x} \ln (1+ax)\)

Aplicando límite a ambos lados de la ecuación se tiene: \[ \lim_{x \to 0} \ln y = \lim_{x \to 0} \frac{b}{x} \ln (1+ax) \] Calculando el límite de la derecha de la igualdad tenemos una forma indeterminada de producto: \[ \lim_{x \to 0} \frac{b}{x} \ln (1+ax) = \frac{b}{0} \ln(1+a \times 0) \] \[ \Rightarrow \infty\ln(1) = \infty \times 0 \] Rescribiendo la expresión se tiene: \[ \lim_{x \to 0} \frac{b}{x} \ln (1+ax) = \lim_{x \to 0} \frac{b \ln(1+ax)}{x} \] \[ \Rightarrow \frac{b\ln(1)}{0} = \frac{b \times 0}{0} = \frac{0}{0}\] Por lo que se sugiere aplicar la regla del L'Hôpital. De esta manera se tiene: \[ \lim_{x \to 0} \frac{b \ln(1+ax)}{x} = \lim_{x \to 0} \frac{ab}{\frac{1+ax}{1}} \] \[ \Rightarrow \lim_{x \to 0} \frac{ab}{1+ax} = \frac{ab}{1+a(0)} = ab \] Por lo tanto: \[ \lim_{x \to 0} ( 1 + ax)^{\frac{b}{x}} = e^{ab} \]

Ejercicios complementarios de la sección.

1. Calcular el límite si es que existe: \[ \lim_{x \to 0^{+}} \left( 1 + \frac{1}{x} \right)^{x} \] Evaluando el límite tenemos que: \[ \lim_{x \to 0^{+}} \left( 1 + \frac{1}{x} \right)^{x} = \left( 1 + \frac{1}{0} \right)^{0} = (1+\infty)^{0} = \infty^{0} \] De donde: \[ y = \left( 1 + \frac{1}{x} \right)^{x} \Rightarrow \ln{y} = \ln{\left( 1 + \frac{1}{x} \right)^{x}} = x\ln{\left( 1 + \frac{1}{x} \right)} \] Calculando el límite: \[ \lim_{x \to 0^{+}} \ln{y} = \lim_{x \to 0^{+}} x\ln{\left( 1 + \frac{1}{x} \right)} = 0 \ln{\left( 1 + \frac{1}{0} \right)} = 0 \times \infty \] Se obtuvo una indeterminación de producto, por lo que debemos expresar a la función como un cociente y calcular el límite. Así: \[\lim_{x \to 0^{+}} x\ln{\left( 1 + \frac{1}{x} \right)} = \lim_{x \to 0^{+}} \frac{\ln{\left( 1 + \displaystyle\frac{1}{x} \right)}}{\displaystyle\frac{1}{x}} \] \[ = \frac{\ln{\left( 1 + \displaystyle\frac{1}{0} \right)}}{\displaystyle\frac{1}{0}} = \frac{\infty}{\infty} \] Se obtuvo una indeterminación de cociente, por lo que se puede aplicar la Regla de L'Hôpital: \[ \lim_{x \to 0^{+}} \frac{\ln{\left( 1 + \displaystyle\frac{1}{x} \right)}}{\displaystyle\frac{1}{x}} = \lim_{x \to 0^{+}} \frac{\displaystyle\frac{1}{\left( 1 + \displaystyle\frac{1}{x} \right)} \left( 0 - \displaystyle\frac{1}{x^{2}} \right)}{-\displaystyle\frac{1}{x^{2}}} \] \[ \lim_{x \to 0^{+}} \frac{\displaystyle\frac{1}{\left( 1 + \displaystyle\frac{1}{x} \right)} \left( - \displaystyle\frac{1}{x^{2}} \right)}{-\displaystyle\frac{1}{x^{2}}} = \lim_{x \to 0^{+}} \frac{1}{\left( 1 + \displaystyle\frac{1}{x} \right)} \] \[ = \lim_{x \to 0^{+}} \frac{1}{\left( 1 + \displaystyle\frac{1}{x} \right)} = \frac{1}{\left( 1 + \displaystyle\frac{1}{0} \right)} = \frac{1}{(1+\infty)} \] \[ \frac{1}{\infty} = 0 \] Así, el límite quedaría como sigue: \[ \lim_{x \to 0^{+}} \ln{y} = 0 \Rightarrow \lim_{x \to 0^{+}} y = e^{0} = 1 \] Por lo tanto, el límite es igual a: \[ \lim_{x \to 0^{+}} \left( 1 + \frac{1}{x} \right)^{x} = 1 \]

2. Determine el valor del límite si es que existe: \[ \lim_{x \to \infty} (x)^{\frac{1}{x}} \] Evaluando el límite vemos que obtenemos una indeterminación de potencia: \[ \lim_{x \to \infty} (x)^{\frac{1}{x}} = \infty^{0} \] \[ \lim_{x \to \infty} y = \lim_{x \to \infty} (x)^{\frac{1}{x}} \] Aplicando logaritmo natural tenemos que: \[ \ln \Rightarrow \lim_{x \to \infty} \ln{y} = \lim_{x \to \infty} \ln{(x)^{\frac{1}{x}}} \] Por leyes de logaritmos tenemos: \[ \lim_{x \to \infty} \ln{y} = \lim_{x \to \infty} \frac{\ln{x}}{x} = \frac{\infty}{\infty} \] Vemos que obtenemos una indeterminación de cociente, por lo que podemos aplicar la regla de L'hopital: \[ \ln{y} = \lim_{x \to \infty} \frac{\displaystyle\frac{1}{x}}{1} = \lim_{x \to \infty} \frac{1}{x} = 0 \] \[ \Rightarrow \ln{y} = 0 \Rightarrow y = e^{0} \] Por lo tanto: \[ y=1 \] En la gráfica siguiente se observa que cuando \(x\) se aproxima a infinito, la función \( y = x^{\frac{1}{x}} \) se aproxima a \(1\).