1.4 Aplicaciones de la integral definida.
1.4.5 Longitud de arco.
Si queremos conocer el largo de una curva, si dicha curva es una recta podemos calcularla como la distancia entre dos puntos. Pero si la curva no es una recta, no conocemos un procedimiento, por lo que en esta sección nos enfocaremos en este caso.
Consideremos una función \(f(x)\) definida en un intervalo \([a, b]\), tal y como se muestra a continuación:

Para determinar la longitud de la curva que define a la función, consideremos una partición del intervalo \([a, b]\) en \(n\) sub-intervalos de longitud \(\Delta x\) con \(\Delta x = \frac{b-a}{n}\). Considerando el intervalo \([x_{i-1}, x_{i}]\) y si tomamos el rectángulo que se genera hacia la función se tiene lo que se observa en la siguiente figura:

El rectángulo nos determina en su parte superior una aproximación a la curva, segmento que está marcado con rojo, aunque este está muy alejado del valor real. Pero si en vez de tomar el segmento en rojo tomamos el segmento en amarillo, el cual está entre los puntos \(P_{i-1}(x_{i-1}, f(x_{i-1}))\) y \(P_{i}(x_{i}, f(x_{i}))\) se obtiene una aproximación más cercana a la longitud de la curva en este intervalo. Razón por la cual, en vez de tomar el rectángulo sobre cada intervalo, vamos a tomar el trapecio que se forma.

Entonces, determinemos la longitud \(L_{i}\) de la curva en este intervalo, tomando en cuenta que la longitud \(L_{i}\) es igual a la distancia entre los puntos \(P_{i-1}\) y \(P_{i}\) tenemos que: \[ L_{i} = d(P_{i-1}, P_{i}) \] Sustituyendo en la fórmula de la distancia entre dos puntos: \[ L_{i} = \sqrt{ (x_{i} - x_{i-1})^2 + ( f(x_{i}) - f(x_{i-1}) )^2 } \] Necesitamos buscar la forma de modificar la longitud ya que para que podamos llegar a la Suma de Riemann y posteriormente la integral necesitamos tener una expresión por \(\Delta x\). Sin el factor \(\Delta x\) no podemos llegar a la Suma de Riemann. Para esto, usaremos el Teorema del Valor Medio el cual nos dice que: \[ f(b) - f(a) = f'(c)(b-a) \:\:donde\:\: c \in [a, b] \] Si aplicamos el Teorema del Valor Medio para \(f(x)\) en el intervalo \([x_{i-1}, x_{i}]\), tenemos \[ f(x_{i}) - f(x_{i-1}) = f'(x_{i}^*)(x_{i}-x_{i-1}) \:\:con\:\: x_{i}^* \in [x_{i-1}, x_{i}] \] Así, sustituyendo en la fórmula de la distancia entre dos puntos tenemos que: \begin{array}{rcl} L_{i} &=& \sqrt{ (x_{i} - x_{i-1})^2 + ( f'(x_{i}^*)(x_{i}-x_{i-1}) )^2 } \\ L_{i} &=& \sqrt{ (x_{i} - x_{i-1})^2 + ( f'(x_{i}^*) )^2 (x_{i}-x_{i-1})^2 } \\ L_{i} &=& \sqrt{ (x_{i} - x_{i-1})^2 ( 1 + (f'(x_{i}^*))^2 ) } \\ L_{i} &=& \sqrt{ 1 + (f'(x_{i}^*))^2 } (x_{i} - x_{i-1}) \\ L_{i} &=& \sqrt{ 1 + (f'(x_{i}^*))^2 } \Delta x \\ \end{array} Como en esta última expresión ya tenemos \(\Delta x\), para aproximarnos a la longitud de la curva \(f(x)\) en \([a, b]\), calculamos las longitudes de cada sub-intervalo. Gráficamente tenemos lo siguiente:

De modo que: \begin{align} L_{1} &=& \sqrt{ 1 + (f'(x_{1}^*))^2 } \Delta x \\ L_{2} &=& \sqrt{ 1 + (f'(x_{2}^*))^2 } \Delta x \\ &\vdotswithin{=} \notag \\ L_{i} &=& \sqrt{ 1 + (f'(x_{i}^*))^2 } \Delta x \\ &\vdotswithin{=} \notag \\ L_{n} &=& \sqrt{ 1 + (f'(x_{n}^*))^2 } \Delta x \\ \end{align} Luego: \[ L \approx \sum_{i=1}^{n} \sqrt{ 1 + (f'(x_{i}^*))^2 } \Delta x \] Tomando el límite cuando \(n\) tiende a \(\infty\), tenemos: \[ L = \lim_{h\to\infty} \sum_{i=1}^{n} \sqrt{ 1 + (f'(x_{i}^*))^2 } \Delta x \] De donde: \[ L = \int_{a}^{b} \sqrt{ 1 + (f'(x))^2 } \, dx \]
Sea \(f\) una función suave o alisada en \([a, b]\), esto es \(f'(x)\) continua en \([a, b]\), la longitud de la curva \(y = f(x)\) para \(a \leq x \leq b\), es: \[ L = \int_{a}^{b} \sqrt{ 1 + (f'(x))^2 } \, dx \] Como región \(y\) y sea \(f\) una función suave o alisada en \([c, d]\), esto es \(f'(y)\) continua en \([c, d]\), la longitud de la curva \(x = f(y)\) para \(c \leq y \leq d\), es: \[ L = \int_{c}^{d} \sqrt{ 1 + (f'(y))^2 } \, dy \]
Si encontramos que la función \(y = f(x)\) no es suave en \(x=a\) o en \(x=b\), podemos tomar la función \(x=f(y)\) y mostrar que es suave en esta variable para \([c, d]\). Si la función no es suave en cualquier punto interior del intervalo \([a, b]\) o en \([c, d]\) no es posible calcular la longitud de la curva. Cuando se calcula la longitud de la curva no es necesario graficar la función.
Ejemplo.
Calcular la longitud de arco de la curva \(y = \left( \frac{x}{2} \right)^\frac{2}{3} \) desde \(x=0\) hasta \(x=2\).
Primero determinemos si la función \(f(x) = (\frac{x}{2}) ^\frac{2}{3} \) es suave. \[ f'(x) = \left( \frac{1}{2^\frac{2}{3}} \right) \left( \frac{2}{3} x^{ - \frac{1}{3}} \right) = \frac{ 2^{\frac{1}{3}} }{ 3x^{ \frac{1}{3}} }, f'(x) \:\:no\:\:es\:\:continua\:\:para\:\:x=0 \] Veamos que sucede si cambiamos la variable, esto es que consideremos la función \(x=f(y)\), despejando \(x\) de la expresión \(y = (\frac{x}{2}) ^\frac{2}{3} \), tenemos que: \[ y = \left( \frac{x}{2} \right)^\frac{2}{3} \implies y^{ \frac{3}{2} } = \frac{x}{2} \implies x = 2y^{ \frac{3}{2} } \implies f(y) = 2y^{\frac{3}{2}} \] El intervalo para \(y\), queda determinado si evaluamos los valores de \(x\) en la nueva función \(f(y)\): \begin{array}{rcl} Si\:\: x=0 &\implies& y = \left( \frac{0}{2} \right)^{ \frac{2}{3} } &=& 0 \\ Si\:\: x=2 &\implies& y = \left( \frac{2}{2} \right)^{ \frac{2}{3} } &=& 1 \end{array} Por lo que \(y\) varia de \(y=0\) hasta \(y=1\). Ahora, comprobaremos que la función \(f(y) = 2y^{\frac{3}{2}}\) sea suave: \[ f'(y) = 2 \left( \frac{3}{2} y^{\frac{1}{2}} \right) = 3y^{\frac{1}{2}} = 3\sqrt{y} \] Por lo tanto, concluimos que la función \(f'(y)\) es continua en \([0, 1]\), luego la función es suave.
Como último paso, calcularemos la longitud de la curva. \[ L = \int_{0}^{1} \sqrt{1+(3\sqrt{y})^2} \:\:dy = \int_{0}^{1} \sqrt{1+9y} \:\:dy \] Resolviendo la integral tenemos que: \[ \int_{0}^{1} \sqrt{1+9y} \:\:dy \:\:\:\: u = 1+9y \:\:\:\: du = 9\,dy \] \[ \frac{1}{9} \int_{0}^{1} \sqrt{u} \:\:du = \frac{1}{9} \left( \frac{2}{3} (u)^{\frac{3}{2}} \right)\Big|_{0}^{1} \] Sustituyendo el valor del cambio de variable, \(u = 1+9y\) \[ \frac{1}{9} \left( \frac{2}{3} (1+9y)^{\frac{3}{2}} \right)\Big|_{0}^{1} = \frac{2}{27}(1+9y)^{\frac{3}{2}} \Big|_{0}^{1} \] \[ \Rightarrow \frac{2}{27}(1+9)^{\frac{3}{2}} - \frac{2}{27}(1)^{\frac{3}{2}} = \frac{2}{27}(10)^{\frac{3}{2}} - \frac{2}{27} \] \[ \Rightarrow \frac{2}{27}(10\sqrt{10} - 1) = 2.26 \:\:unidades. \] Finalmente, la longitud de arco de la curva \(y = \left( \frac{x}{2} \right)^\frac{2}{3} \) es \(2.26 \:\:unidades\).
Área de superficie de sólidos.
Una superficie de revolución se obtiene al girar una curva llamada generatriz alrededor de una recta que se utiliza como eje en el plano. Un ejemplo de esto se obtiene al girar una circunferencia alrededor de su diámetro obteniendo una esfera. Muchas de las superficies simétricas que conocemos pueden generarse utilizando una única curva que describe el comportamiento de su contorno, ejemplo de ello son: huevo, jarrón, botella, trompo, etc

Determinemos la forma de calcular el área de superficie que se genera al girar una función \(y=f(x)\) con respecto al eje \(x\), supongamos que es una función no negativa y con derivada \(f'(x)\) continua en \([a,b]\).

Para determinar el área de la superficie del sólido que se obtiene al girar la función con respecto al eje \(x\), consideremos una partición del intervalo \([a,b]\) en \(n\) sub-intervalos de longitud \(\Delta x\), con \(\Delta x = \frac{b-a}{n} \). Considerando el intervalo \([x_{i-1}, x_{i}]\) y si además tomamos el segmento de recta que se tiene entre los puntos \(P (x_{i-1}, f(x_{i-1})) \) y \(Q (x_{i}, f(x_{i})) \) se forma un trapecio, mismo que observamos en la sección de longitud de arco que es más cercano a la curva, entonces, se tiene que:

Al girar el trapecio obtenemos un cono truncado, y éste tiene un área de superficie \(S_{i}\). Ahora, procederemos a anotar los datos correspondientes de dicho cono de la siguiente manera:

El área de superficie \(S\) de un cono truncado es \(S = 2\pi\times(radio\:\:medio)\times(longitud\:\: generatriz)\), la generatriz es la distancia entre \(P\) y \(Q\), es decir: \[ radio\:\:medio = \frac{f(x_{i-1}) + f(x_{i})}{2} \] \[ longitud\:\:generatriz = L_{PQ} = Longitud\:\:de\:\:arco\:\:entre\:\:los\:\:puntos\:\:P\:\:y\:\:Q \] \[ longitud\:\:gene ratriz = \sqrt{ 1 + (f'(x_{i}^*))^2 } \Delta x \] Así el área de superficie del cono truncado en el intervalo \([x_{i-1}, x_{i}]\), es: \[ S_{i} = 2\pi \left( \frac{f(x_{i-1}) + f(x_{i})}{2} \right) \sqrt{ 1 + (f'(x_{i}^*))^2 } \Delta x \]
Calculando el área de superficie de los conos trucados que se generan sobre cada sub-intervalo y sumándolas tenemos: \[ S \approx \sum_{i=1}^{n} 2\pi \left( \frac{f(x_{i-1}) + f(x_{i})}{2} \right) \sqrt{ 1 + (f'(x_{i}^*))^2} \Delta x \] Tomando el límite cuando \(n\) tiende a infinito, tenemos que el área de superficie es: \[ S = \lim_{n\to\infty} \sum_{i=1}^{n} 2\pi \left( \frac{f(x_{i-1}) + f(x_{i})}{2} \right) \sqrt{ 1 + (f'(x_{i}^*))^2} \Delta x \] \[ S = \int_{a}^{b} 2\pi \left( \frac{f(x) + f(x)}{2} \right) \sqrt{ 1 + (f'(x))^2} \,dx \] \[ S = \int_{a}^{b} 2\pi f(x) \sqrt{ 1 + (f'(x))^2} \,dx \]
Sea \(f\) una función suave o alisada en \([a, b]\), esto es \(f'(x)\) continua en \([a, b]\), el área \(S\) de la superficie generada al girar la gráfica de \(y=f(x)\) para \(a \leq x \leq b\), alrededor del eje \(x\), es: \[ S = \int_{a}^{b} 2\pi f(x) \sqrt{ 1 + (f'(x))^2} \,dx \] Siendo \(f(x)\) el radio medio medio del cono truncado que se genera.
Como región \(y\) y sea \(f\) una función suave o alisada en \([c, d]\), esto es \(f'(y)\) continua en \([c, d]\), el área \(S\) de la superficie generada al girar la gráfica de \(x=f(y)\) para \(c \leq y \leq d\), alrededor del eje \(y\), es: \[ S = \int_{c}^{d} 2\pi f(y) \sqrt{ 1 + (f'(y))^2} \,dy \]
Ejemplo 1.
Calcular el área de la superficie generada al girar la región limitada \(y = cosh\,x\) desde \(x=0\) hasta \(x=2\), con respecto al eje \(x\).

En este caso el radio coincide con la función, luego \(y = f(x) = cosh\,x\) y los límites nos lo dan en el planteamiento del problema por lo que \(x\) varia de \(0\) a \(1\), por lo que el siguiente paso es determinar si la función es suave: \[ f'(x) = sinh\,x \] Como \(f'(x)\) es continua para todo \(x\), la función \(f(x)\) es suave. Finalmente, calculemos el área de superficie: \[ S = \int_{0}^{1} 2\pi \,cosh\,x \sqrt{ 1 + (sinh\,x)^2} \,dx = \int_{0}^{1} 2\pi \,cosh\,x \sqrt{cosh^2\,x} \,dx \] \[ \Rightarrow \int_{0}^{1} 2\pi \,cosh\,x \,cosh\,x \,dx = \int_{0}^{1} 2\pi cosh^2\,x \,dx \] \[ \Rightarrow 2\pi \int_{0}^{1} \frac{cosh\,2x + 1}{2} \,dx = \pi \int_{0}^{1} (cosh\,2x + 1) \,dx \] \[ \Rightarrow \pi \left( \frac{1}{2} sinh\,2x + x \right) \Big|_{0}^{1} = \pi \left( \frac{1}{2} sinh\,2 + 1 - \frac{1}{2} sinh\,0 - 0 \right) \] \[ \Rightarrow \pi \left( \frac{1}{2} sinh\,2 + 1 \right) = 8.8386 \] Por lo tanto, el área de superficie de la región limitada por \(y =cosh\,x\) desde \(x=0\) hasta \(x=2\) es: \[ S = 8.8386 \]
Ejemplo 2.
La forma del reflector de un faro se obtiene haciendo girar una parábola alrededor de su eje. Calcular el área de la superficie de un reflector que mide \(4\) pies de diámetro y tiene una profundidad de \(1\) pie.

El reflector del faro se obtiene de una parábola que podemos situar su centro en el origen, de la siguiente manera:
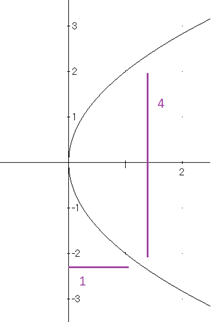
Vemos que la parábola pasa por los puntos \((1, 2)\) y \((1, -2)\) , podemos determinar la ecuación de la parábola con centro en el origen que pasa por esos puntos.
La ecuación de la parábola con centro en el origen que abre hacia la derecha es: \[ y^{2} = 4px \] Como el punto \((1, 2)\) se encuentra en la parábola, para ese punto se cumple igualdad, así \[ (2)^{2} = 4p(1) \Rightarrow 4 = 4p \Rightarrow p = 1 \] Luego la función es \(y^{2} = 4x\), esto es \(y=\pm 2 \sqrt{x}\)
Pero como queremos una función de \(x\), que gire con respecto al eje \(x\), es suficiente con la parte superior de la parábola o con la raíz positiva, así: \[ y = f(x) = 2\sqrt{x} \] Veamos si la función es suave en \( (0, 1) \): \[ y' = \frac{2}{2\sqrt{x}} = \frac{1}{\sqrt{x}} \] Esta función es continua en el intervalo \( (0, 1) \) , por lo tanto es suave.
Cabe destacar que el cero no está incluido porque el intervalo es abierto. Determinemos el área de superficie: \[ S = \int_{0}^{1} 2\pi(2\sqrt{x}) \sqrt{1+\left( \frac{1}{\sqrt{x}} \right)^{2}} \,dx = 4\pi \int_{0}^{1} (\sqrt{x}) \sqrt{1+\frac{1}{x} } \,dx \] \[ = 4\pi \int_{0}^{1} \sqrt{x} \sqrt{\frac{x+1}{x} } \,dx = 4\pi \int_{0}^{1} \sqrt{x} \frac{\sqrt{x+1}}{\sqrt{x}} \,dx \] \[ = 4\pi \int_{0}^{1} \sqrt{x+1} \,dx = \frac{8\pi}{3}(x+1)^{\frac{3}{2}} \Bigg|_{0}^{1} \] \[ = \frac{8\pi}{3} (1+1)^{\frac{3}{2}} - \frac{8\pi}{3} (0+1)^{\frac{3}{2}} \] \[ = \frac{8\pi}{3} (2)^{\frac{3}{2}} - \frac{8\pi}{3} (1)^{\frac{3}{2}} \] \[ = \frac{8\pi}{3} \Big( (2)^{\frac{3}{2}} - 1 \Big) = \frac{8\pi}{3} (2\sqrt{2} - 1) \] Por lo tanto, el área de la superficie es: \[ A = \frac{8\pi}{3} (2\sqrt{2} - 1) \]
Ejemplo 3.
El arco de la parábola \(y=x^{2}\) de \((1, 1)\) a \((2, 4)\) se hace girar en torno al eje \(y\), tal y como se muestra a continuación. Encuentre el área de la superficie resultante.
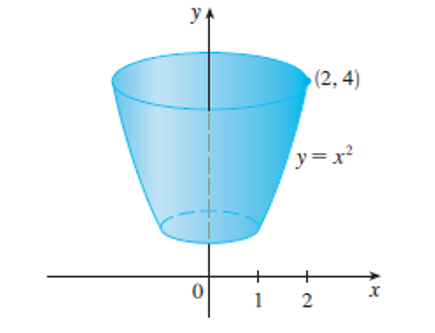
Solución 1. Revisamos si la derivada de la función es continua en el intervalo dado. \[ x = \sqrt{y} \;\;entonces\;\; \frac{dx}{dy} = \frac{1}{2\sqrt{y}} \] Planteamos la fórmula para determinar el área de la superficie: \[ S = 2\pi \int_{1}^{4} \sqrt{y} \sqrt{1+ \left( \frac{1}{2\sqrt{y}} \right)^{2}}\,dy \] Resolvemos la integral: \[ S = 2\pi \int_{1}^{4} \sqrt{y} \sqrt{1+ \frac{1}{4y}}\,dy = 2\pi \int_{1}^{4} \sqrt{y} \sqrt{ \frac{4y+1}{4y}}\,dy \] \[ = 2\pi \int_{1}^{4} \frac{\sqrt{y}}{2\sqrt{y}} \sqrt{4y+1} \,dy = \pi \int_{1}^{4} \sqrt{4y+1} \,dy \] \[ = \frac{\pi}{4} \int_{1}^{4} u^{\frac{1}{2}} \,du = \frac{\pi}{4} \frac{2}{3}(4y+1)^{\frac{3}{2}} \Bigg|_{1}^{4} \] \[ \frac{\pi}{6} \Big((16+1)^{\frac{3}{2}} - (5)^{\frac{3}{2}}\Big) \] \[ S = \frac{\pi}{6} (17\sqrt{17} - 5\sqrt{5}) \approx 9.81\pi \]
Solución 2. Utilizando \(y=x^{2}\) y \( \displaystyle\frac{dy}{dx} = 2x \) \[ S = \int 2\pi x \,dx \] \[ S = \int_{1}^{2} 2\pi \sqrt{1+ \left( \frac{dy}{dx} \right)^{2}} \,dx \] \[ S = 2\pi \int_{1}^{2} x \sqrt{1+4x^{2}} \,dx \] Al sustituir \( u=1+4x^{2} \), se tiene \(du=8x\). Recuerda que al cambiar los límites de integración, se tiene: \[ S = \frac{\pi}{4} \int_{5}^{17} \sqrt{u} \,du = \frac{\pi}{4} \Bigg[ \frac{2}{3} u^{\frac{3}{2}} \Bigg]\Bigg|_{5}^{17} \] \[ S = \frac{\pi}{6}(17\sqrt{17} - 5\sqrt{5}) \approx 9.81\pi \] Como podemos observar, llegamos al mismo valor obtenido en la solución 1. Por lo tanto, el área de la superficie resultante es: \[ S = \frac{\pi}{6}(17\sqrt{17} - 5\sqrt{5}) \approx 9.81\pi \]