2.2 Integrales impropias
2.2.2 Integrales impropias con límites de integración infinitos
1. Si \(f\) es continua en el intervalo \( [a,\infty) \), entonces: \[ \int_{a}^{\infty} f(x) \,dx = \lim_{b \to \infty} \int_{a}^{b} f(x) \,dx \] 2. Si \(f\) es continua en el intervalo \( (-\infty,b] \), entonces: \[ \int_{-\infty}^{b} f(x) \,dx = \lim_{a \to -\infty} \int_{a}^{b} f(x) \,dx \] Se dice que la integral impropia converge si el límite existe, en caso contrario, la integral impropia diverge.
Ejemplo 1. Integral impropia con límite de integración infinito
Determinar si la integral \(\int_{1}^{\infty} \frac{dx}{x}\) converge o diverge. El integrando es \(f(x) = \frac{1}{x} \), el cual es una función continua en el intervalo \([1, \infty)\), usando la definición tenemos: \[ \int_{1}^{\infty} \frac{1}{x} \,dx = \lim_{b \to \infty} \int_{1}^{b} \frac{1}{x} \,dx \] \[\Rightarrow \lim_{b \to \infty} [\ln(x)]\Big|_{1}^{b} = \lim_{b \to \infty} (\ln(b) - ln(1)) \] \[\Rightarrow \lim_{b \to \infty} \ln(b) = \infty \] Por lo tango, la integral \(\int_{1}^{\infty} \frac{dx}{x}\) diverge.
Ejemplo 2. Determinar si la siguiente integral es convergente o divergente
\[ \int_{-\infty}^{0} \frac{dx}{2x-5} \] Como primer paso se obtienen las raíces del denominador del integrando, para saber con qué valor se hace discontinua la función: \begin{array}{rcl} 2x - 5 &=& 0 \\ 2x &=& 5 \\ x &=& \frac{5}{2} \\ \end{array} El integrando es discontinuo para \(x=\frac{5}{2}\), sin embargo, este punto está fuera de los límites de integración, por lo tanto, se puede resolver la integral. \[ \lim_{ n \to -\infty } \int_{n}^{0} \frac{dx}{2x-5} \] Observamos que esta integral se resuelve por cambio de variable, por lo que decimos que: \[ u=2x-5 \:;\: du\,=2\,dx \] \[ \lim_{ n \to -\infty } \frac{1}{2} \int_{n}^{0} \frac{du}{u} \] \[ \lim_{ n \to -\infty } \frac{1}{2} [\ln u]\Big|_{n}^{0} \] Volviendo a la variable original: \[ \lim_{ n \to -\infty } \frac{1}{2} [\ln (2x-5)]\Big|_{n}^{0} \] Evaluando la integral: \[ \lim_{ n \to -\infty } \frac{1}{2} [\ln (2(0)-5) - \ln (2n-5) ] \] \[ \Rightarrow \frac{1}{2} [\ln (-5) - \ln (2(-\infty)-5) ] \] Obtenemos los valores de \(\ln(-5)\) y \(\ln(-\infty-5)\), pero sabemos que \( \ln(-5) = \ln(5)\) y además que: \[ \ln(-\infty-5) = \ln(-\infty) = \ln(\infty) = \infty\] entonces se tiene lo siguiente: \[\frac{1}{2} [\ln(5) - \infty]\] A su vez, sabemos que \(\ln(5) \lll -\infty \) por lo que la resta se desprecia, obteniendo así: \[ \lim_{ n \to -\infty } \int_{n}^{0} \frac{dx}{2x-5} = -\infty \] Por lo tanto, decimos que la integral diverge.
Ejemplo 3. Determinar si la siguiente integral es convergente o divergente
\[ \int_{-\infty}^{0} x e^{x} \,dx \] El integrando es \(f(x) = x e^{x}\) el cual es una función continua en el intervalo \( (-\infty, 0] \), usando la definición tenemos: \[ \int_{-\infty}^{0} x e^{x} \,dx = \lim_{ a \to -\infty } \int_{a}^{0} x e^{x} \,dx \] Integrando por partes, haciendo \( u=x, \: du\,=\,dx \:\:y\:\: dv\,=e^x \,dx,\,v=e^x\) obtenemos: \[ \int x e^{x} \,dx = x e^{x} - \int e^x \,dx = x e^x - e^x \] Luego: \[ \lim_{ a \to -\infty } \int_{a}^{0} x e^{x} \,dx = \lim_{ a \to -\infty } (x e^x - e^x)\Big|_{a}^{0} \] \[ \Rightarrow \lim_{ a \to -\infty } [(0e^0 - e^0) - (ae^a - e^a)] = \lim_{ a \to -\infty } (-1-ae^a+e^a) \] \[ \Rightarrow \lim_{ a \to -\infty } -1 - \lim_{ a \to -\infty } ae^a + \lim_{ a \to -\infty } e^a \] Calculando los límites tenemos que \(\lim\limits_{a \to \infty} -1 = -1\) y \(\lim\limits_{a \to \infty} e^a = e^{-\infty}\), es decir hay que determinar el valor del límite de la función exponencial cuando \( x \to -\infty\), para esto utilizaremos la gráfica de la función \(e^x\).
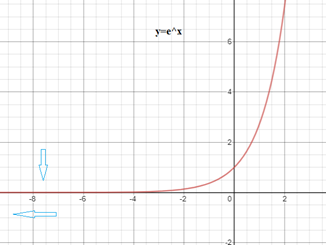
Observamos que, si los valores de \(x\) decrecen, esto es si tienden a \(- \infty\), los valores de \(y\) se aproximan a cero, esto es \(\lim\limits_{x \to -\infty} e^x = 0 \), así \(\lim\limits_{a \to -\infty} e^a = 0 \).
Por último evaluaremos el límite: \[ \lim\limits_{a \to -\infty} -ae^a = -(-\infty)e^{-\infty} = \infty \times 0 \] Vemos que al evaluar el límite no tenemos un resultado como en los otros casos, obtenemos una forma indeterminada, por lo que hay que resolverla. Primero, representaremos el producto como un cociente: \[ \lim_{a \to -\infty} -ae^a = \lim_{a \to -\infty} -\frac{a}{e^{-a}} \] Aplicamos la regla de L'Hôpital: \[ \lim_{a \to -\infty} -\frac{a}{e^{-a}} = \lim_{a \to -\infty} - \left( \frac{1}{-e^{-a}} \right) \] \[ \Rightarrow \lim_{a \to -\infty} - \left( \frac{1}{-e^{-a}} \right) = \lim_{a \to -\infty} e^a = 0 \] Luego: \[ \lim_{ a \to -\infty } -1 - \lim_{ a \to -\infty } ae^a + \lim_{ a \to -\infty } e^a = -1 + 0 + 0 = -1 \] Por lo tanto: \[ \int_{-\infty}^{0} x e^{x} \,dx = -1 \] La integral converge y su valor es \(-1\)
Ejemplo 4. ¿Cómo calculamos el valor de la siguiente integral?
\[ \int_{-\infty}^{\infty} \frac{1}{1+x^2} \,dx\] En este caso no podemos usar ninguno de los dos casos de la definición ya que infinito no solo es el límite inferior o superior sino ambos y además, no tenemos que la función es continua en un intervalo semi-abierto como \([a,\infty)\) o \((-\infty, b]\). Para este tipo de integrales donde los dos límites de integración son infinitos y donde la función es continua en \((-\infty, \infty)\), se tiene la siguiente definición.
Si \(f\) es continua en el intervalo \( (-\infty,\infty) \) y si tanto \( \int_{-\infty}^{c} f(x) \, dx \) y \( \int_{c}^{\infty} f(x) \, dx \) convergen, decimos que \( \int_{-\infty}^{\infty} f(x) \, dx \) converge, y se determina su valor como: \[ \int_{-\infty}^{\infty} f(x) \,dx = \int_{-\infty}^{c} f(x) \,dx + \int_{c}^{\infty} f(x) \,dx \] Donde \(c\) es un número real, si alguna de las integrales \( \int_{-\infty}^{c} f(x) \, dx \:\) y \(\: \int_{c}^{\infty} f(x) \, dx \) diverge entonces la \( \int_{-\infty}^{\infty} f(x) \,dx \) diverge.
Una vez entendemos la definición, podemos calcular el límite planteado anteriormente. El integrando \(f(x) = \frac{1}{1+x^2} \) es continuo en \( (-\infty, \infty) \), luego decimos que la función \( f(x) = \frac{1}{1+x^2} \) es continua en \( (-\infty, c] \) y en \( [c, \infty) \). De tal modo que si \( f(x) = \frac{1}{1+x^2} \) es continua en \( (-\infty, c] \), entonces tenemos que: \[ \int_{-\infty}^{c} \frac{1}{1+x^2} \,dx = \lim_{a \to -\infty} \int_{a}^{c} \frac{1}{1+x^2} \,dx \] \[ \Rightarrow \lim_{a \to -\infty} arctan \,x \Big|_{a}^{c} = \lim_{a \to -\infty} (arctan \, c - arctan \,a) \] \[ \Rightarrow arctan \, c - \lim_{a \to -\infty} arctan \,a \] El límite de la función trigonométrica inversa lo determinamos a partir de su gráfica:
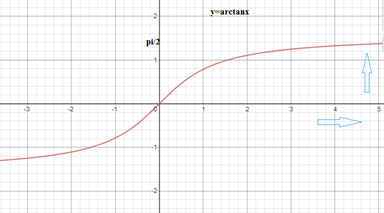
Apartir de la gráfica tenemos que \( \lim\limits_{x \to -\infty} arctan \,x = -\frac{\pi}{2} \) y \( \lim\limits_{x \to \infty} arctan \,x = \frac{\pi}{2} \), por lo tanto, el valor de la integral es: \[ \int_{-\infty}^{c} \frac{1}{1+x^2} \,dx = arctan \, c - \left( -\frac{\pi}{2} \right) = arctan \, c + \frac{\pi}{2} \] Determinemos el valor de la otra integral.
Como \( f(x) = \frac{1}{1+x^2} \) es continua en \( [c, \infty) \), entonces \[ \int_{c}^{\infty} \frac{1}{1+x^2} \,dx = \lim_{b \to \infty} \int_{c}^{b} \frac{1}{1+x^2} \,dx \] \[ \Rightarrow \lim_{b \to \infty} arctan \,x \Big|_{c}^{b} = \lim_{b \to \infty} (arctan\,b - arctan\,c) \] \[ \Rightarrow \lim_{b \to \infty} arctan\,b - arctan\,c = \frac{\pi}{2} - arctan\,c \] Anteriormente determinamos el valor del límite en infinito, luego: \[ \int_{-\infty}^{\infty} \frac{1}{1+x^2} \,dx = arctan\,c + \frac{\pi}{2} + \frac{\pi}{2} - arctan\,c = \pi \] Concluimos entonces que la integral converge a \(\pi\) .
De acuerdo con la definición: \[ \int_{-\infty}^{\infty} f(x) \,dx = \int_{-\infty}^{c} f(x) \,dx + \int_{c}^{\infty} f(x) \,dx \] donde \(c\) es un número real. Podemos tomar a \(c\) como cualquier número real de tal manera que al evaluar la integral nos dé un valor conocido, así podemos decir que \(c = 0\), de tal modo que se divida en la integral de números negativos y de números positivos.