2.1 Formas indeterminadas
2.1.1 Introducción
Cuando determinamos el límite de una función \(\lim\limits_{x \to a} f(x)\), podemos tener alguno de los siguientes casos: \[ 1.\:\: \lim_{x \to a} f(x) \:es\:igual\:a\:un\:número\:real \] \[ 2.\:\: \lim_{x \to a} f(x) \:no\:existe \] \[ 3.\:\: \lim_{x \to a} f(x) \:\:es\:una\:forma\:indeterminada \] Las dos primeras opciones dan solución al límite, pero la tercera no, así que cuando nos encontramos con una forma indeterminada necesitamos realizar algún procedimiento que nos permita determinar el valor del límite de la función y remover la forma indeterminada que presenta.
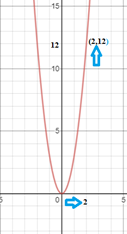
Para el primer caso, consideremos que queremos calcular el límite de \(\lim\limits_{x \to 2} 3x^2 = 12\), cuando la función \(3x^2\) se aproxima a \(12\), tal y como lo podemos observar en la siguiente figura:
Cuando el límite de una función no existe puede deberse a alguno de los siguientes casos:
- Cuando los límites unilaterales existen pero no son iguales.
- Cuando la función toma un valor de \(\infty\), generalmente se trata de una asíntota.
- Cuando la funcoón tiene un comportamiento oscilatorio, tales como las funciones trigonométricas.
Finalmente, el tercer caso se refiere a una indeterminación como los cocientes \(\frac{\infty}{\infty}\) o \(\frac{0}{0}\), la indeterminación se puede remover empleando alguna técnica algebraica, como factorizar, dividir entre la variable de mayor exponente, usar racionalización, emplear división sintética, como se muestra en la siguiente situación:
\(\lim\limits_{x \to \infty} \frac{x^2-1}{x+1} = \frac{\infty}{\infty}\); al hacer el cálculo se obtiene una indeterminación de cociente.
\(\lim\limits_{x \to \infty} \frac{x^2-1}{x+1} = \frac{\infty}{\infty}\); se remueve la indeterminación empleando factorización.
\(\lim\limits_{x \to \infty} \frac{(x+1)(x-1)}{x+1}\); se cancelan términos semejantes.
\(\lim\limits_{x \to \infty} (x-1) = \infty \); al hacer el cálculo se obtiene \(\infty\), por lo tanto, el límite no existe. Gráficamente, tenemos lo siguiente:
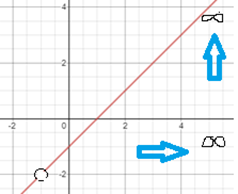
Se observa que la función \(y= \frac{x^2-1}{x+1}\) es una función racional y al dividir el numerador entre el denominador se obtiene la función \(y= (x-1)\) cuya representación gráfica es una línea recta. Como podemos observar en la gráfica en el punto \((-1,-2)\) hay un hueco, pero es continua en todos los demás puntos. Asimismo, se observa que cuando el valor de \(x\) tiende a infinito, la función también tiende a infinito.
Enseguida tenemos otro ejemplo en este caso al remover la indeterminación se obtiene un número real.
\(\lim\limits_{x \to \infty} \frac{3x^2-x-2}{5x^2+4x+1} = \frac{\infty}{\infty}\); al hacer el cálculo se obtiene una indeterminación de cociente.
Se divide entre la \(x\) de mayor exponente: \[ \lim_{x \to \infty} \frac{\frac{3x^2-x-2}{x^2}}{\frac{5x^2+4x+1}{x^2}}\ \] Se efectúan las divisiones: \[ \lim_{x \to \infty} \frac{\frac{3x^2}{x^2}-\frac{x}{x^2}-\frac{2}{x^2}}{\frac{5x^2}{x^2}+\frac{4x}{x^2}+\frac{1}{x^2}} \] Se realiza el cálculo: \[ \lim_{x \to \infty} \frac{3-\frac{1}{x}-\frac{2}{x^2}}{5+\frac{4}{x}+\frac{1}{x^2}} = \frac{3}{5} \]
Por lo tanto: \[ \lim_{x \to \infty} \frac{3x^2-x-2}{5x^2+4x+1} = \frac{3}{5} \]
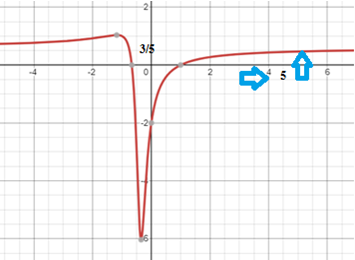
En la gráfica de la función racional \(y= \frac{3x^2-x-2}{5x^2+4x+1}\) se observa que cuando \(x\) se aproxima a \(5\), esta función se aproxima a \(\frac{3}{5}\).
Hasta aquí se ha hecho un repaso sobre la indeterminación que se usa en el cálculo de límites de funciones, pero hay más formas indeterminadas:
| Tipos de indeterminación | |||
| Cociente | Producto | Diferencia | Potencia |
| \(\frac{0}{0}, \frac{\infty}{\infty} \) | \(0 \times \infty\) | \( \infty - \infty \) | \( 0^0, 1^{\infty}, \infty^{0} \) |