2.1 Formas indeterminadas
2.1.4 Diferencia indeterminada
Definición. Una diferencia indeterminada se obtiene cuando al evaluar el límite de la función, obtenemos la forma \( \infty - \infty \) , en este caso no se puede emplear ninguna regla operatoria para límites, por lo que la estrategia de solución es modificar algebraicamente la función para convertirla a un cociente, lo que nos permite usar la Regla de L’Hôpital.
Ejemplo 1. Determinar el valor del límite si es que existe.
\[ y = \lim_{x \to \frac{\pi}{2}^{-}} ( \sec x - \tan x) \] En la función \(\sec x\) como en la de \(\tan x\) cuando el valor de \(x\) se aproxima a \(\frac{\pi}{2}\) por la izquierda, ambas funciones tienden a \(\infty\), tal y como podemos observar a continuación:
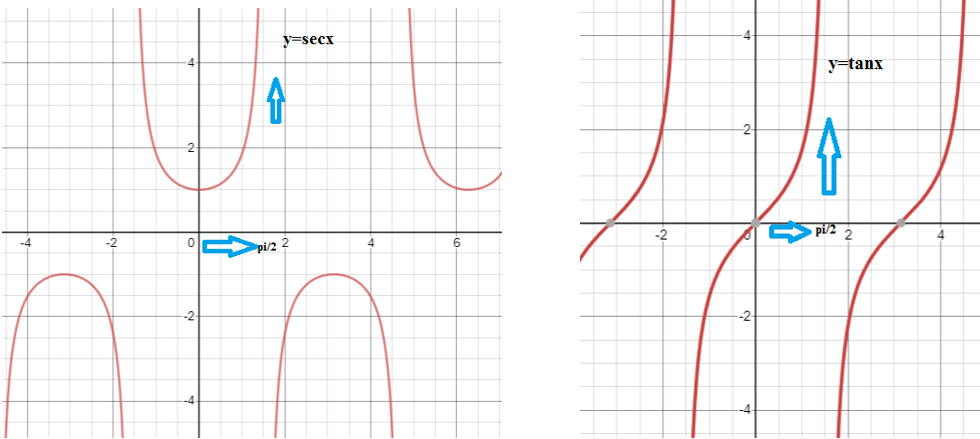
De modo que al evaluar el límite tenemos que: \[ y = \lim_{x \to \frac{\pi}{2}^{-}} ( \sec x - \tan x) = ( \infty - \infty ) \] Aplicando propiedades trigonométricas podemos transformar en cociente a la función para aplicar la regla de L'Hôpital. \[ y = \lim_{x \to \frac{\pi}{2}^{-}} \frac{1}{\cos x} - \frac{\sin x}{\cos x} = \frac{1 - \sin x}{\cos x} = \frac{0}{0} \] Finalmente, aplicamos la regla de L'Hôpital y evaluamos el límite: \[ \lim_{x \to \frac{\pi}{2}^{-}} \frac{1 - \sin x}{\cos x} = \lim_{x \to \frac{\pi}{2}^{-}} \frac{-\cos x}{- \sin x} = \frac{0}{1} = 0 \] Por lo tanto: \[ y = \lim_{x \to \frac{\pi}{2}^{-}} ( \sec x - \tan x) = 0 \]
En la siguiente gráfica se observa que cuando \(x\) se aproxima por la izquierda a \(\frac{\pi}{2}\) la función \(y = \sec x - \tan x\) se aproxima a cero.
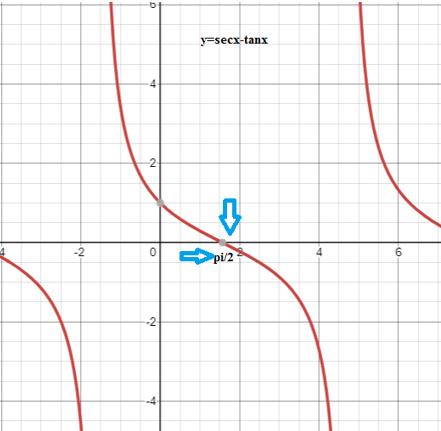
Ejercicios complementarios de la sección.
1. Determinar el valor del límite si es que existe: \[ \lim_{x \to 0^{+}} (\csc{x}-\cot{x}) \] Si evaluamos el límite tenemos que: \[ \lim_{x \to 0^{+}} (\csc{x}-\cot{x}) = \csc{0^{+}} - \cot{0^{+}} \] Para determinar el valor de las funciones trigonométricas en cero veamos las gráficas de las funciones a continuación:
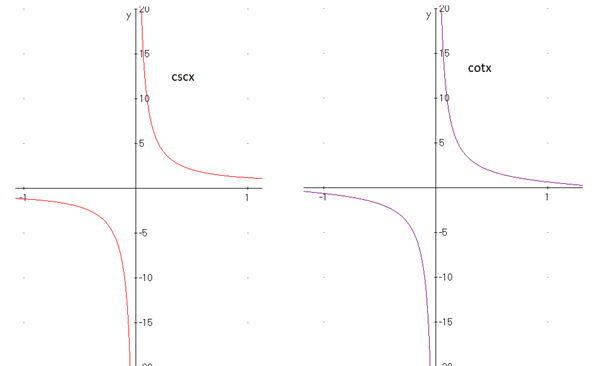
Cuando nos aproximamos a cero por la derecha, ambas funciones crecen, por lo que el límite será infinito. Luego entonces: \[ \lim_{x \to 0^{+}} (\csc{x}-\cot{x}) = \csc{0^{+}} - \cot{0^{+}} = \infty - \infty \] Hay que pasar a un cociente la diferencia de funciones y como son funciones trigonométricas, entonces las identidades trigonométricas nos dan esta posibilidad, por lo que quedaría de la siguiente manera: \[ \lim_{x \to 0^{+}} (\csc{x}-\cot{x}) = \lim_{x \to 0^{+}} \left( \frac{1}{\sin{x}} - \frac{\cos{x}}{\sin{x}} \right) \] \[ = \lim_{x \to 0^{+}} \frac{1-\cos{x}}{\sin{x}} = \frac{1-\cos{(0)}}{\sin{(0)}} = \frac{1-1}{0} = \frac{0}{0} \] Como se obtuvo un cociente indeterminado, podemos aplicar la Regla de L'Hôpital: \[ \lim_{x \to 0^{+}} \frac{1-\cos{x}}{\sin{x}} = \lim_{x \to 0^{+}} \frac{\sin{x}}{\cos{x}} = \frac{\sin{(0)}}{\cos{(0)}} \] \[ \Rightarrow \frac{0}{1} = 0 \] Por lo tanto, el límite es igual a: \[ \lim_{x \to 0^{+}} (\csc{x}-\cot{x}) = 0 \]
2. Determinar el valor del límite si es que existe: \[ \lim_{x \to \infty} \Big( \ln{(2x)} - \ln{(x+1)} \Big) \] Si evaluamos tenemos lo siguiente: \[ \lim_{x \to \infty} \Big( \ln{(2x)} - \ln{(x+1)} \Big) = \ln{(\infty)} - \ln{(\infty)} = \infty - \infty \] Recordemos que el \( \lim\limits_{x \to \infty} \ln{x} = \infty \) debido a que cuando \(x\) crece también lo hace \( \ln{x} \). Para resolver el límite necesitamos pasar a un cociente, en este caso vemos el tipo de función y revisamos si alguna propiedad algebraica nos lleva a determinar un cociente, por lo que aplicando las leyes de los logaritmos tenemos: \[ \ln{a} - \ln{b} = \ln{\frac{a}{b}} \] Esto nos da la posibilidad de representar como un cociente a la diferencia de los logaritmos que se tiene en la función. Así: \[ \lim_{x \to \infty} \Big( \ln{(2x)} - \ln{(x+1)} \Big) = \lim_{x \to \infty} \ln{\Big(\frac{2x}{x+1}\Big)} \] Si evaluamos el límite tenemos que: \[ \lim_{x \to \infty} \ln{\Big(\frac{2x}{x+1}\Big)} = \ln{\Big(\frac{2(\infty)}{\infty+1}\Big)} \neq \frac{\infty}{\infty} \] El aplicar la propiedad no nos lleva a la forma indeterminada para poder aplicar la Regla de L'Hôpital, pero tenemos el Teorema siguiente:
Si \(f\) y \(g\) son funciones tales que \( \lim\limits_{x \to a} g(x) = b \), y si \(f\) es continua en \(b\), entonces: \[ \lim_{x \to a} f\Big(g(x)\Big) = f(b) = f\Big( \lim_{x \to a} g(x) \Big) \] Este teorema nos permite intercambiar la función y el límite, siempre y cuando la función sea continua.
Podemos aplicar el teorema anterior debido a que la función logaritmo natural es continua. \[ \lim_{x \to \infty} \ln{\Big(\frac{2x}{x+1}\Big)} = \ln\left( \lim_{x \to \infty} \frac{2x}{x+1} \right) \] Calculamos el límite de la función y vemos que obtenemos una indeterminación de cociente. \[ \lim_{x \to \infty} \frac{2x}{x+1} = \frac{2(\infty)}{(\infty)+1} = \frac{\infty}{\infty} \] Aplicamos la Regla de L'Hôpital y tenemos que: \[ \lim_{x \to \infty} \frac{2x}{x+1} = \lim_{x \to \infty} \frac{2}{1} = 2 \] Finalmente, regresamos a la expresión que teníamos anteriormente: \[ \ln\left( \lim_{x \to \infty} \frac{2x}{x+1} \right) = \ln{(2)} \] Por lo tanto: \[ \lim_{x \to \infty} \Big( \ln{(2x)} - \ln{(x+1)} \Big) = \ln{(2)} \]