3.4 Series Alternantes

3.4.4 Convergencia Condicional

Ejemplo 1.

Mostrar que la serie \( \sum\limits_{n=1}^{\infty} (-1)^{n-1} \displaystyle\frac{1}{n} \) converge condicionalmente.

La serie de los valores absolutos es: \[ \sum_{n=1}^{\infty} \bigg| (-1)^{n-1} \frac{1}{n} \bigg| = \sum_{n=1}^{\infty} \bigg| (-1)^{n-1} \bigg| \bigg| \frac{1}{n} \bigg| \] Tomando en cuenta que \(|(-1)^{n-1}|\) es \(1\): \[ \Rightarrow \sum_{n=1}^{\infty} \bigg| \frac{1}{n} \bigg| = \sum_{n=1}^{\infty} \frac{1}{n} \] La serie resultante es la serie armónica y sabemos que diverge. Luego la serie de los valores absolutos diverge, pero la serie original, ¿converge? o ¿diverge?, al tratarse de una serie alternante, podemos determinar su convergencia. \[ \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n} \] \[ \Rightarrow b_{n} = \frac{1}{n} \] i) Si \( f(x) = \frac{1}{x} \), derivando \( f'(x) = - \frac{1}{x^2} \lt 0 \; \forall n \), luego la función es decreciente y se cumple la primera condición del criterio.

ii) Si \( \lim\limits_{n \to \infty} \frac{1}{n} = 0 \) con lo que se cumple la segunda condición del criterio.

Por lo tanto, la serie: \[ \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n} \; converge. \] Y por el criterio de convergencia condicional la serie converge condicionalmente.

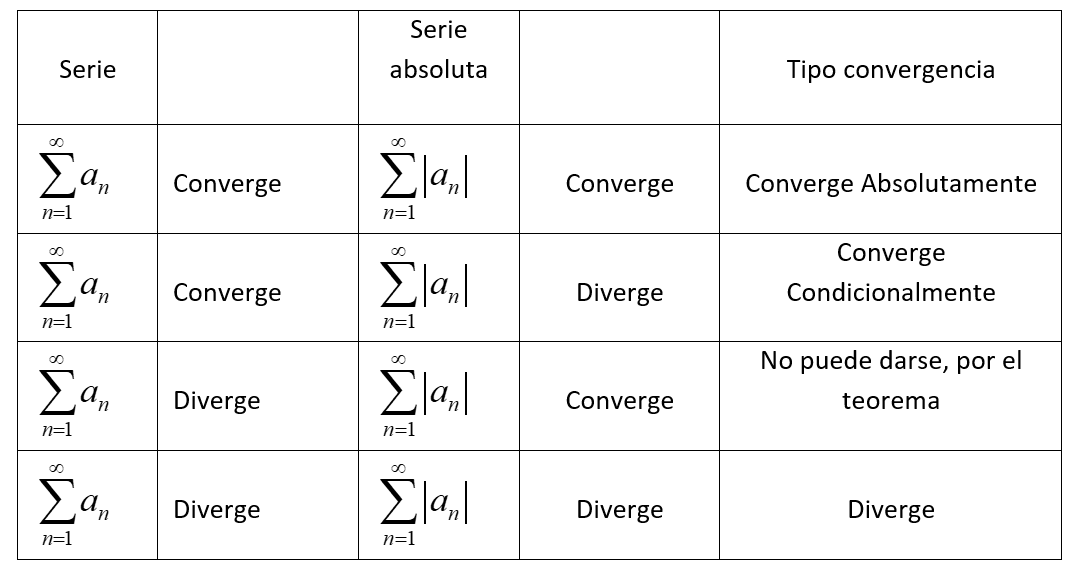
Con las definiciones de convergencias condicional y absoluta tenemos los casos de convergencia que se muestran en la tabla siguiente:

Ejemplo 2.

Menciona si la serie es absolutamente convergente, condicionalmente convergente o divergente. \[ \sum_{n=1}^{\infty} \frac{(-1)^{n}}{n^{4}} \] Por el criterio de la razón tenemos lo siguiente: \[ \Bigg| \frac{a_{n+1}}{a_{n}} \Bigg| = \Bigg| \frac{\displaystyle\frac{(-1)^{n+1}}{(n+1)^{4}}}{\displaystyle\frac{(-1)^{n}}{n^{4}}} \Bigg| = \Bigg| \frac{(-1)^{n} (-1) n^{4}}{(n+1)^{4}(-1)^{n}} \Bigg| = \frac{n^{4}}{(n+1)^{4}} \] \[ \lim_{n \to \infty} \Bigg| \frac{a_{n+1}}{a_{n}} \Bigg| = \lim_{n \to \infty} \frac{n^{4}}{(n+1)^{4}} = \lim_{n \to \infty} \frac{\displaystyle\frac{n^{4}}{n^{4}}}{ \left( \displaystyle\frac{n}{n} + \frac{1}{n} \right)^{4} } \] \[ = \lim_{n \to \infty} \frac{1}{\left( 1 + \displaystyle\frac{1}{n} \right)^{4}} = 1 \] Como \( \lim\limits_{n \to \infty} \Bigg| \displaystyle\frac{a_{n+1}}{a_{n}} \Bigg| = 1 \), el criterio de la razón no es concluyente.

Por el criterio de la convergencia absoluta tenemos que: \[ \sum_{n=1}^{\infty} \Bigg| \frac{(-1)^{n}}{n^{4}} \Bigg| = \sum_{n=1}^{\infty} \frac{1}{n^{4}} \] Se trata de una serie P con \(p=4 \gt 1\), por lo tanto la serie original es es absolutamente convergente. \[ \sum_{n=1}^{\infty} \frac{(-1)^{n}}{n^{4}} \]

Ejemplo 3.

Determina el tipo de convergencia de la serie: \[ \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1+n}{n^{2}} \] Hay que determinar si la serie converge absolutamente, converge condicionalmente o diverge. Podemos empezar determinando la convergencia de los valores absolutos, ya que si converge, de acuerdo con el teorema, converge también la serie original y con eso daremos solución al problema. \[ \sum_{n=1}^{\infty} \Bigg| (-1)^{n-1} \frac{1+n}{n^{2}} \Bigg| = \sum_{n=1}^{\infty} \frac{1+n}{n^{2}} \] Vemos que se trata de una serie de términos positivos, y además es una función racional, es decir, polinomio en el numerador y en denominador, por lo que podemos usar el criterio de comparación por limite, tomando \(a_{n}\) y \(b_{n}\) como: \[ a_{n} = \frac{1+n}{n^{2}} \;\;y\;\; b_{n} = \frac{n}{n^{2}} = \frac{1}{n} \] Nos damos cuenta que la serie de \(b_{n}\) es la serie armónica y sabemos que diverge. \[ \sum_{n=1}^{\infty} b_{n} = \sum_{n=1}^{\infty} \frac{1}{n} \] Determinemos el límite: \[ \lim_{n \to \infty} \frac{\displaystyle\frac{1+n}{n^{2}}}{\displaystyle\frac{1}{n}} = \lim_{n \to \infty} \frac{n(1+n)}{n^{2}} \] \[ = \lim_{n \to \infty} \frac{1+n}{n} = \lim_{n \to \infty} \frac{1}{n} + 1 = 1 \gt 0 \] Luego por el criterio de comparación por limite las dos series convergen o divergen y como \( \sum\limits_{n=1}^{\infty} b_{n} \) diverge, la serie \( \sum\limits_{n=1}^{\infty} \displaystyle\frac{1+n}{n^{2}} \) diverge.

Hay que determinar la convergencia de la serie: \[ \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1+n}{n^{2}} \] Esta es una serie alternante, verifiquemos si converge o diverge tomando \( b_{n} = \displaystyle\frac{1+n}{n^{2}} \)

i) Sea \( f(x) = \displaystyle\frac{1+x}{x^{2}} \), calculando la derivada tenemos que: \[ f'(x) = \frac{x^{2}(1)-2x(1+x)}{x^{4}} = \frac{x^{2}-2x-2x^{2}}{x^{4}} \] \[ = \frac{-x^{2}-2x}{x^{4}} \lt 0 \;\;\forall\; x \gt 0 \] decimos entonces que la función \(f\) es decreciente y se cumple la primera condición. ii) Determinemos el límite: \[ \lim_{n \to \infty} \frac{1+n}{n^{2}} = \lim_{n \to \infty} \left( \frac{1}{n^{2}} + \frac{n}{n^{2}} \right) \] \[ \lim_{n \to \infty} \left( \frac{1}{n^{2}} + \frac{1}{n} \right) = \frac{1}{\infty^{2}} + \frac{1}{\infty} = 0 \] Al cumplirse la segunda condición, la serie original converge, luego entonces, la serie: \[ \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1+n}{n^{2}} \] converge condicionalmente.