3.4 Series Alternantes
3.4.3 Convergencia Absoluta
Una serie \( \sum\limits_{n=1}^{\infty} a_{n} \) converge absolutamente o es absolutamente convergente si la serie correspondiente de los valores absolutos converge. Esto es, si \[ \sum_{n=1}^{\infty} |a_{n}| = |a_{1}| + |a_{2}| + ⋯ + |a_{n}| + ⋯ \; converge \]
En general si tenemos una serie alternante \( \sum\limits_{n=1}^{\infty} (-1)^{n-1} b_{n} \), la serie de los valores absolutos es: \[ \sum_{n=1}^{\infty} \bigg|(-1)^{n-1} b_{n}\bigg| = \sum_{n=1}^{\infty} \bigg|(-1)^{n-1}\bigg| \bigg|b_{n}\bigg| \] Por la propiedad de valor absoluto, el valor absoluto del producto es igual al producto de los valores absolutos. Y como \( \bigg|(-1)^{n-1}\bigg| = 1 \) ya que independientemente de que el exponente sea par o impar, \((-1)^{n-1}\) es \(1\) o \(-1\) y el valor absoluto de este es \(1\). \[ \sum_{n=1}^{\infty} \bigg|(-1)^{n-1} b_{n}\bigg| = \sum_{n=1}^{\infty} \bigg|(-1)^{n-1}\bigg| \bigg|b_{n}\bigg| = \sum_{n=1}^{\infty} \bigg|b_{n}\bigg| \] Cuando definimos la serie alternante se puso como condición en la definición que \(b_{n} \gt 0\), así \( |b_{n}| = b_{n} \), por lo que \[ \sum_{n=1}^{\infty} \bigg|b_{n}\bigg| = \sum_{n=1}^{\infty} b_{n} \]
Ejemplo 1.
La serie: \[ \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n^2} \] converge absolutamente, esto es debido a que la serie de los valores absolutos es igual a \[ \sum_{n=1}^{\infty} \bigg| (-1)^{n-1} \frac{1}{n^2} \bigg| = \sum_{n=1}^{\infty} \bigg| (-1)^{n-1} \bigg| \bigg| \frac{1}{n^2} \bigg| \] Tomando en cuenta que \(|(-1)^{n-1}|\) es \(1\): \[ \Rightarrow \sum_{n=1}^{\infty} \bigg| \frac{1}{n^2} \bigg| = \sum_{n=1}^{\infty} \frac{1}{n^2} \] La serie resultante es una Serie P con \( p = 2 \gt 1\), por lo tanto converge.
📖 Teorema. Si una serie \( \sum\limits_{n=1}^{\infty} a_{n} \) es absolutamente convergente, entonces la serie \( \sum\limits_{n=1}^{\infty} a_{n} \) converge.
Este teorema nos proporciona una estrategia para determinar si una serie que no sea de valores positivos o alternante converge, ya que basta con que se tome la serie de los valores absolutos y si esta converge entonces la serie original también converge.
Ejemplo 2.
Determinar si la serie dada converge o diverge. \[ \sin{1} + \frac{\sin{2}}{2^2} + \frac{\sin{3}}{3^2} + ⋯ + \frac{\sin{n}}{n^2} + ⋯ \] Para aplicar algún criterio debemos de determinar el tipo de serie. Veamos el signo que tienen los términos, el denominador es positivo ya que es el cuadrado de un número entero positivo, así el signo depende del numerador de la función que es la función \( \sin{n} \), para ello veamos la gráfica de la función:

En esta gráfica notamos que \(\sin{1}\), \(\sin{2}\) y \(\sin{3}\) son mayores que cero y que \(\sin{4}\), \(\sin{5}\) y \(\sin{6}\) son negativos, ¿será que el signo se intercala de 3 en 3 elementos? Veamos la gráfica en otro intervalo
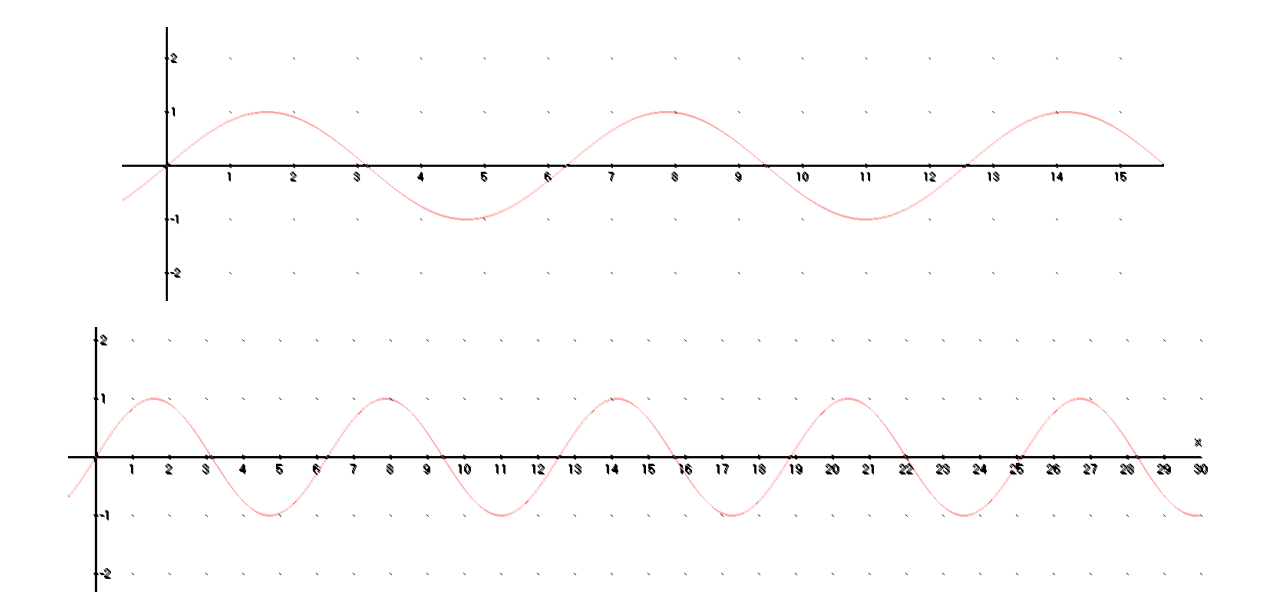
Los valores de \(\sin{22}\), \(\sin{23}\), \(\sin{24}\) y \(\sin{25}\) son negativos, es decir, en este intervalo ya no se tienen 3 valores con el mismo signo sino 4. Por lo cual no hay regularidad en los valores de la serie, de modo que no es una serie de términos positivos y no es una serie alternante. No podemos aplicar los criterios conocidos para determinar su convergencia o divergencia, así que usaremos la convergencia absoluta y el teorema anterior. \[ \sin{1} + \frac{\sin{2}}{2^2} + \frac{\sin{3}}{3^2} + ⋯ + \frac{\sin{n}}{n^2} + ⋯ = \sum_{n=1}^{\infty} \frac{\sin{n}}{n^2} \] La serie de los valores absolutos queda expresada de la siguiente manera: \[ \sum_{n=1}^{\infty} \bigg| \frac{\sin{n}}{n^2} \bigg| = \sum_{n=1}^{\infty} \frac{|\sin{n}|}{n^2} \] esta es una serie de términos positivos y para determinar su convergencia o divergencia podemos usar cualquiera de los criterios para este tipo de serie, en este caso usaremos el criterio básico de comparación: \[ |\sin{n}| \leq 1\] \[ \frac{|\sin{n}|}{n^2} \leq \frac{1}{n^2}\] Así \(a_{n}\) y \(b_{n}\) son iguales a: \[ a_{n} = \frac{|\sin{n}|}{n^2} \;y\; b_{n} = \frac{1}{n^2} \] Determinemos si la serie \( \sum b_{n} \) converge o diverge. \[ \sum_{n=1}^{\infty} b_{n} = \sum_{n=1}^{\infty} \frac{1}{n^2} \] Vemos que se trata de una Serie P con \( p = 2 \lt 1 \), por lo que la serie converge. Por lo tanto la serie: \[ \sum_{n=1}^{\infty} b_{n} = \sum_{n=1}^{\infty} \frac{1}{n^2} \; converge \] Y además se cumple que: \[ a_{n} = \frac{|\sin{n}|}{n^2} \leq \frac{1}{n^2} = b_{n} \] Por el criterio básico de comparación concluimos que la serie: \[ \sum_{n=1}^{\infty} \frac{|\sin{n}|}{n^2} \; converge \] Como es la serie de los valores absolutos se tiene que la serie: \[ \sum_{n=1}^{\infty} \frac{\sin{n}}{n^2}\] converge absolutamente y por el teorema la serie converge.