1.4 Aplicaciones de la integral definida.

1.4.2 Área entre curvas.

Ahora, nos concentraremos en calcular el área de una región comprendida entre las gráficas de dos funciones integrables \(f\) y \(g\). Consideremos, en primer lugar, la situación de siguiente gráfica:

Queremos calcular el área comprendida entre los gráficos de \(f\) y \(g\) para \(a \leq x \leq b\). En este caso, \(f(x) \geq g(x)\) para todo \(x \in [a, b]\). Como puede verse en los gráficos siguientes, el área \(A\) resulta ser la diferencia entre 2 áreas: el área \(A_{1}\) de la región comprendida entre el gráfico de \(f\) y el eje \(x\) para \(a \leq x \leq b\) y el área \(A_{2}\) de la región comprendida entre el gráfico de \(g\) y el eje \(x\) para \(a \leq x \leq b\).

Si bien anteriormente consideramos el caso que \(f\) y \(g\) son funciones no negativas en el intervalo \([a,b]\), la fórmula anterior vale siempre que \(f\) y \(g\) cumplan que \(f(x) \geq g(x)\), aunque tomen valores negativos. Para ver esto, consideremos la siguiente gráfica:

En este caso, ambas funciones \(f\) y \(g\) toman valores positivos y negativos en el intervalo \([a,b]\). Observemos que el área de la región no cambia si la trasladamos (manteniendo su forma y dimensiones). Como la región es acotada, haciendo una traslación en sentido vertical, podemos conseguir que toda la región quede por encima del eje \(x\) y, en consecuencia, reducimos al caso ya analizado. Para hacer esta traslación, basta con sumar una constante \(k\) suficientemente grande, a \(f\) y a \(g\), de manera que \(g(x) + K \geq 0\) para todo \(x \in [a, b]\) y entonces, \(f(x) + K \geq g(x) + K \geq 0\) para toda \(x \in [a, b]\). Gráficamente, tenemos lo siguiente:

Así, el áre de la región es: \[ A = \int_{a}^{b} [(f(x) + K) - (g(x) + K)] \,dx = \int_{a}^{b} [f(x) - g(x)] \,dx \] En resumen. Si bien la integral tiene varias aplicaciones una de las más comunes es su uso para encontrar áreas entre curvas o entre funciones. Para esto nos basaremos en la fórmula: \[ A = \int_{a}^{b} [f(x) - g(x)] \,dx \] Si a la hora de graficar nuestras funciones nos conviene usar rectángulos verticales, es decir, si usamos rectángulos horizontales usaremos la fórmula: \[ A = \int_{a}^{b} [f(y) - g(y)] \,dy \]

Ejemplo 1.

Calcular el área de la región encerrada entre las gráficas de \( f(x)=3x^2-2 \) y \( g(x)=2x-1 \)

Para empezar, haremos una gráfica aproximada de la región cuya área queremos calcular.

La región está limitada por los valores de \(x\) correspondientes a los dos puntos en los que se intersectan los gráficos de \(f\) y \(g\); es decir, los valores de \(x\) para los cuales \(f(x) = g(x)\). Calculemos estos valores igualando ambas funciones: \begin{array}{rcl} f(x) &=& g(x) \\ 3x^2-2 &=& 2x-1 \end{array} Despejando \(x\) tenemos que: \begin{array}{rcl} 3x^2-2-2x+1 &=& 0 \\ (3x+1)\:\:(x-1) &=& 0 \end{array} Entonces, los valores de \(x\) que delimitan el área son \(x = 1\) y \(x = - \frac{1}{3}\). Como podemos observar en la siguiente gráfica, \(g(x) \geq f(x) \) para todo \(x \in [- \frac{1}{3}; 1]\).

Por lo tanto, el área de la región encerrada entre los gráficos de \(f\) y \(g\) es: \begin{array}{rcl} A &=& \int_{-\frac{1}{3}}^{1} [g(x) - f(x)] \,dx = \int_{-\frac{1}{3}}^{1} (2x-1-(3x^2-2)) \,dx \\ &\Rightarrow& \int_{-\frac{1}{3}}^{1} (-3x^2+2x+1) \,dx = (-x^3+x^2+x)\Big|_{-\frac{1}{3}}^{1} \\ &\Rightarrow& 1 - \left( - \frac{-5}{27}\right) \end{array} Por lo tanto, el área entre las dos funciones es: \[ A = \frac{32}{27} \]

Ejemplo 2.

Encontrar el área comprendida por la función \(f(x) = -x^{2}+4\) y \(g(x) = x^{2}-4\). Comencemos determinando los puntos donde se intersectan las gráficas, para ello igualemos las funciones: \begin{array}{rcl} -x^{2}+4 & = & x^{2}-4 \\ -x^{2}-x^{2}+4+4 & = & 0 \\ -2x^{2}+8 & = & 0 \\ 2x^{2}-8 & = & 0 \\ x^{2}-4 & = & 0 \\ x^{2} & = & 4 \\ x & = & \pm \sqrt{4} \\ x_{1} = 2 & ; & x_{2} = -2 \end{array} Enseguida procedemos a graficar la funciones y tenemos que:

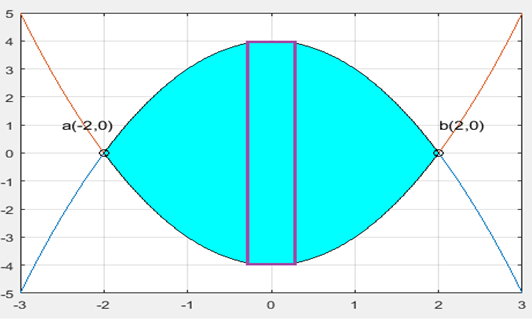
Como nos podemos dar cuenta también nos conviene usar rectángulos verticales ya que de esa manera se tocan ambas funciones. Ahora, planteamos la integral con base en la fórmula. \[ A = \int_{a}^{b} [f(x)-g(x)]\,dx \] \[ A = \int_{-2}^{2} [(-x^{2}+4)-(x^{2}-4)]\,dx \] Finalmente resolvemos la integral. \[ A = \int_{-2}^{2} [(-x^{2}+4)-(x^{2}-4)]\,dx = \int_{-2}^{2} (-2x^{2}+8)\,dx \] \[ \Big[ -\frac{2}{3}x^{3} + 8x \Big]\Bigg|_{-2}^{2} = \Big[ \frac{32}{3} \Big] - \Big[ -\frac{32}{3} \Big] = \frac{64}{3} u^{2} \] Por lo tanto, el área solicitada es: \[ A = \frac{64}{3} u^{2} \]

Ejemplo 3.

Encontrar el área comprendida por la función \(f(x) = x+4\) y \(g(x) = x^{2}-2\). Lo primero que se tiene que hacer es igualar nuestras funciones para ver donde se interceptan y de esa manera podamos encontrar nuestros límites para aplicar nuestra fórmula. \begin{array}{rcl} x+4 & = & x^{2}-2 \\ x^{2}-x-2-4 & = & 0 \\ x^{2}-x-6 & = & 0 \\ (x-3)(x+2) & = & 0 \\ x_{1} = 3 & ; & x_{2} = -2 \end{array} Una vez encontrados nuestros puntos de intersección es 100% recomendable graficar las funciones para saber qué área calcularemos.

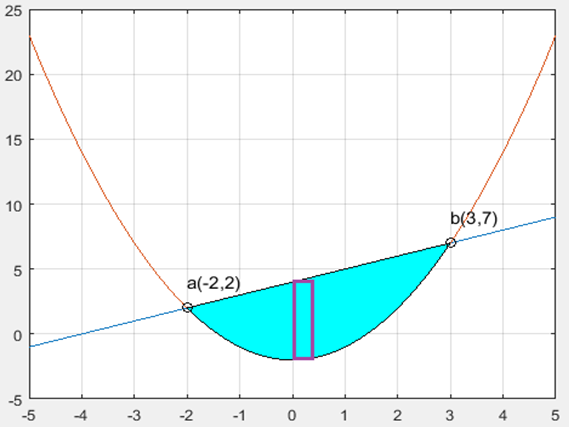
Ya tenemos nuestra gráfica y cómo podemos observar nos conviene usar rectángulos verticales ya que tocan ambas funciones, por lo que procedemos a plantear nuestra fórmula para el área. \[ A = \int_{a}^{b} [f(x)-g(x)]\,dx \] \[ A = \int_{-2}^{3} [(x+4)-(x^{2}-2)]\,dx \] Finalmente resolvemos la integral y de esa forma se obtiene el área deseada. \[ A = \int_{-2}^{3} [(x+4)-(x^{2}-2)]\,dx = \int_{-2}^{3} (x+4-x^{2}+2)\,dx \] \[ A = \int_{-2}^{3} (-x^{2}+x+6)\,dx = \Big[ -\frac{x^{3}}{3} + \frac{x^{2}}{2} + 6x \Big]\Bigg|_{-2}^{3} \] \[ A = \Big[ \frac{27}{2} \Big] - \Big[ -\frac{22}{3} \Big] = \frac{125}{6}u^{2} \]